题目内容
5.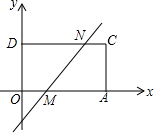 点A的坐标是(4,0),点M是OA上一点,且AM=3OM,把点A向上平移2个单位到点C,过点C作y轴的垂线,垂足为点D.
点A的坐标是(4,0),点M是OA上一点,且AM=3OM,把点A向上平移2个单位到点C,过点C作y轴的垂线,垂足为点D.(1)四边形OACD是矩形;
(2)过点M作直线MN交CD于点N,若MN把四边形OACD面积分成相等的两部分,求直线MN的解析式.
分析 (1)根据DC∥OA,AC∥OD,证得四边形OACD是平行四边形,进而证得四边形OACD是矩形;
(2)根据题意求得M(1,0),N(3,2),然后根据待定系数法即可求得一次函数的解析式.
解答 解:(1)∵CD⊥y轴,
∴DC∥OA,
∵AC∥OD,
∴四边形OACD是平行四边形,
∵∠AOD=90°,
∴四边形OACD是矩形;
故答案为:矩.
(2)∵MN把四边形OACD面积分成相等的两部分,
∴OM=CN,DN=AM,
∵点A的坐标是(4,0),
∴OA=4,
∵AM=3OM,
∴OM=1,AM=3,
∴DN=3,
∴M(1,0),N(3,2),
设直线MN的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{k+b=0}\\{3k+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
∴直线MN的解析式为y=x-1.
点评 本题考查了矩形的判定,待定系数法求一次函数的解析式,求得M、N的坐标是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
10.嘉峪关市约有20.5万人,把近似数205000用科学记数法表示为( )
| A. | 205×103 | B. | 20.5×104 | C. | 2.05×105 | D. | 0.205×106 |
 已知在四边形ABCD中,AD=BC,∠D=∠DCE.求证:四边形ABCD是平行四边形.
已知在四边形ABCD中,AD=BC,∠D=∠DCE.求证:四边形ABCD是平行四边形.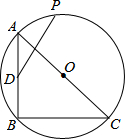 如图,等腰Rt△ABC内接于⊙O,AB=4$\sqrt{2}$,D为AB的中点,P为⊙O上一动点,则线段DP的最大值为4+2$\sqrt{2}$.
如图,等腰Rt△ABC内接于⊙O,AB=4$\sqrt{2}$,D为AB的中点,P为⊙O上一动点,则线段DP的最大值为4+2$\sqrt{2}$.