题目内容
定义新运算:对于任意实数a、b,都有a⊕b=(a+b)(a-b)+2b(a+b),等式右边是通常的加法、减法及乘法运算.比如:2⊕5=(2+5)×(2-5)+2×5×(2+5)=-21+70=49.
(1)求(-2)⊕3的值;
(2)通过计算,验证等式a⊕b=b⊕a成立.
(1)求(-2)⊕3的值;
(2)通过计算,验证等式a⊕b=b⊕a成立.
考点:因式分解的应用,实数的运算
专题:新定义
分析:(1)利用定义新运算的方法直接求得数值即可;
(2)直接代入计算,进一步因式分解得出答案即可.
(2)直接代入计算,进一步因式分解得出答案即可.
解答:解:(1)-2⊕3
=(-2+3)×(-2-3)+2×3×(-2+3)
=1×(-5)+2×3×1
=-5+6
=1;
(2)∵a⊕b
=(a+b)(a-b)+2b(a+b)
=a2-b2+2 ab+2b2
=(a+b)2;
b⊕a
=(b+a)(b-a)+2a(b+a)
=b2-a2+2 ab+2a2
=(a+b)2
所以a⊕b=b⊕a.
=(-2+3)×(-2-3)+2×3×(-2+3)
=1×(-5)+2×3×1
=-5+6
=1;
(2)∵a⊕b
=(a+b)(a-b)+2b(a+b)
=a2-b2+2 ab+2b2
=(a+b)2;
b⊕a
=(b+a)(b-a)+2a(b+a)
=b2-a2+2 ab+2a2
=(a+b)2
所以a⊕b=b⊕a.
点评:此题考查定义新运算的运算方法,以及因式分解的运用,理解题意,掌握运算方法是解决问题的关键.

练习册系列答案
相关题目
 如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;
如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;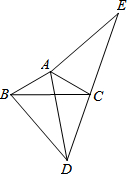 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点C在DE上.求证:
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点C在DE上.求证:
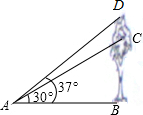 九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)
九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)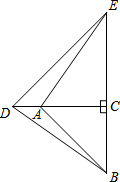 如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD.
如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD.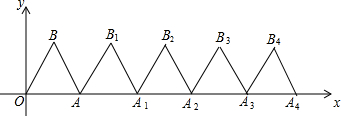 如图,△ABO是边长为6的等边三角形,将△ABO向右平移得第2个等边三角形△A1B1A;再将△A1B1A向右平移得第3个等边三角形△A2B2A1,重复以上做法得到第5个等边三角形△A4B4A3,若P(m,2
如图,△ABO是边长为6的等边三角形,将△ABO向右平移得第2个等边三角形△A1B1A;再将△A1B1A向右平移得第3个等边三角形△A2B2A1,重复以上做法得到第5个等边三角形△A4B4A3,若P(m,2