题目内容
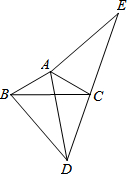 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点C在DE上.求证:
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点C在DE上.求证:(1)△ABD≌△ACE;
(2)∠BDA=∠ADC.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据等式的性质,可得∠BAD=∠CAE,根据SAS,可得两个三角形全等;
(2)根据全等三角形的性质,可得对应角相等,根据等腰三角形的性质,可得∠ADC=∠AEC,根据等量代换,可得证明结论.
(2)根据全等三角形的性质,可得对应角相等,根据等腰三角形的性质,可得∠ADC=∠AEC,根据等量代换,可得证明结论.
解答:证明:(1)∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴∠ADB=∠AEC.
∵AD=AE,
∴∠ADC=∠AEC.
∴∠BDA=∠ADC.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴∠ADB=∠AEC.
∵AD=AE,
∴∠ADC=∠AEC.
∴∠BDA=∠ADC.
点评:本题考查了全等三角形的判定与性质,利用SAS证明三角形全等,利用全等三角形的性质,证明对应角相等,再利用等量代换得出证明结论.

练习册系列答案
相关题目
要使分式
有意义,x的值是( )
| 1 |
| |x|-1 |
| A、x≠1 |
| B、x≠-1 |
| C、-1<x<1 |
| D、x≠1且x≠-1 |