题目内容
4. 不吃早餐会对人的身体造成一定的危害,某校为调查全校学生对“不吃早餐对人的身体造成的危害”的了解程度(分为:基本了解、了解一点、不了解三项),从全校学生中抽取部分学生进行问卷.并将结果制成统计表和条形统计图.
不吃早餐会对人的身体造成一定的危害,某校为调查全校学生对“不吃早餐对人的身体造成的危害”的了解程度(分为:基本了解、了解一点、不了解三项),从全校学生中抽取部分学生进行问卷.并将结果制成统计表和条形统计图.| 了解程度 | 调查人数 | 频率 |
| 基本了解 | a | 0.6 |
| 了解一点 | 15 | n |
| 不了解 | 5 | 0.1 |
(2)a=30,n=0.3;补全条形统计图;
(3)已知该校有3000名学生,学校计划对“了解一点”和“不了解”两类学生进行宣传教育,请问大约有多少名学生要参加这次宣传教育?
(4)学校计划从参加宣传教育的学生中抽取60名学生谈学习体会,求这些学生中的每名学生被抽取的概率是多少?
分析 (1)根据表格中的数据可以求得本次调查的学生数;
(2)根据(1)中的答案可以求得a、n的值,并把统计图补充完整;
(3)根据题意可以估计大约有多少名学生要参加这次宣传教育;
(4)根据(3)中的答案可以求得这些学生中的每名学生被抽取的概率.
解答  解:(1)由题意可得,
解:(1)由题意可得,
本次调查的学生有:5÷0.1=50(名),
故答案为:50;
(2)a=50×0.6=30,n=15÷50=0.3,
故答案为:30,0.3,
补全的条形统计图,如右图所示;
(3)由题意可得,
参加这次宣传教育的学生有:3000×(1-0.6)=1200(名),
答:大约有1200名学生要参加这次宣传教育;
(4)由题意可得,
这些学生中的每名学生被抽取的概率是:$\frac{60}{1200}=\frac{1}{20}$,
答:这些学生中的每名学生被抽取的概率是$\frac{1}{20}$.
点评 本题考查概率公式、用样本估计总体、统计表、条形统计图,解答本题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
17.请借鉴以前研究函数的经验,探索函数y=$\frac{6}{x-1}$+2的图象和性质.
(1)自变量x的取值范围为x≠1;
(2)填写下表,画出函数的图象;
(3)观察图象,写出该函数两条不同类型的性质;
(4)若x>3,则y的取值范围为2<y<5;若y<-1,则x的取值范围为-1<x<1.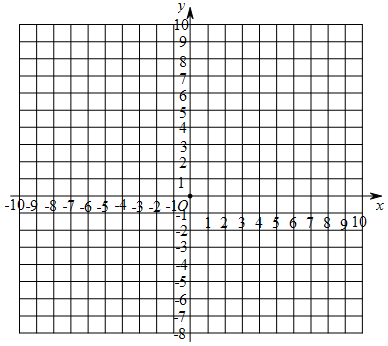
(1)自变量x的取值范围为x≠1;
(2)填写下表,画出函数的图象;
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| y | … | 1 | 0.8 | 0.5 | -1 | -4 | 8 |
(4)若x>3,则y的取值范围为2<y<5;若y<-1,则x的取值范围为-1<x<1.

 如图,已知AB⊥CD,垂足为点O,直线EF经过O点,若∠1=55°,则∠COE的度数为125度.
如图,已知AB⊥CD,垂足为点O,直线EF经过O点,若∠1=55°,则∠COE的度数为125度. 已知:如图,AB∥CD,∠B=∠D,那么AD与BC平行吗?为什么?
已知:如图,AB∥CD,∠B=∠D,那么AD与BC平行吗?为什么? 如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第7个菱形的边长是27.
如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第7个菱形的边长是27. 如图,已知直线AB、CD相交于点O,OE⊥AB,射线OC平分∠AOF,∠BOF=110°,求∠DOE的度数.
如图,已知直线AB、CD相交于点O,OE⊥AB,射线OC平分∠AOF,∠BOF=110°,求∠DOE的度数.