题目内容
19.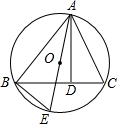 如图,AD是△ABC的高,A,B,C三点在⊙O上,AE是⊙O的直径,△ADC与△ABE相似吗?说明理由.
如图,AD是△ABC的高,A,B,C三点在⊙O上,AE是⊙O的直径,△ADC与△ABE相似吗?说明理由.
分析 根据直径所对的圆周角可得∠ABE=90°,根据高线的定义可得∠ADC=90°,从而得到∠ABE=∠ADC,再根据同弧所对的圆周角相等可得∠E=∠C,然后根据两组角对应相等两三角形相似证明.
解答 解:△ADC与△ABE相似.
理由如下:∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠ABE=∠ADC,
∵∠E、∠C是$\widehat{AB}$所对的圆周角,
∴∠E=∠C,
∴△ADC∽△ABE.
点评 本题考查了相似三角形的判定,圆周角定理,熟练掌握相似三角形的判定方法并确定出两三角形的对应角相等是解题的关键.

练习册系列答案
相关题目
14.若圆的半径为5cm,圆心坐标为(0,0),点P坐标为(4,2),则点P和⊙O的位置关系是( )
| A. | 点P在⊙O外 | B. | 点P在⊙O内 | C. | 点P在⊙O上 | D. | 点P在⊙O外或⊙O上 |




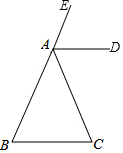 如图,已知AD平分∠EAC,且AD∥BC,求证:AB=AC.
如图,已知AD平分∠EAC,且AD∥BC,求证:AB=AC.