题目内容
9.△ABC中,AB=AC,∠BAC=40°,AD是底边BC边上的中线,BE⊥AC于点E,交AD于点F,则∠DFE 的度数是110°.分析 根据等腰三角形的性质可得∠CAD的度数,根据垂直的定义可得∠AEB=90°,再根据三角形外角的性质可得∠DFE 的度数.
解答  解:∵△ABC中,AB=AC,∠BAC=40°,AD是底边BC边上的中线,
解:∵△ABC中,AB=AC,∠BAC=40°,AD是底边BC边上的中线,
∴∠CAD=$\frac{1}{2}$∠BAC=20°,
∵BE⊥AC,
∴∠AEB=90°,
∴∠DFE=20°+90°=110°.
故答案为:110°.
点评 本题考查了等腰三角形的中线、高和角平分线三线合一的性质,以及垂直的定义,三角形外角的性质,得到∠CAD的度数是解答本题的关键.

练习册系列答案
相关题目
4.下列等式从左到右的变形,属于因式分解的是( )
| A. | m(a+b)=ma+mb | B. | X2+2x+1=x(x+2)+1 | C. | (x+1)(x-1)=x2-1 | D. | x3-x=x(x+1)(x-1) |
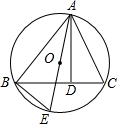 如图,AD是△ABC的高,A,B,C三点在⊙O上,AE是⊙O的直径,△ADC与△ABE相似吗?说明理由.
如图,AD是△ABC的高,A,B,C三点在⊙O上,AE是⊙O的直径,△ADC与△ABE相似吗?说明理由. 如图的三角板中,已知BC=4cm,则AB=8cm.
如图的三角板中,已知BC=4cm,则AB=8cm. 如图,点C是线段AB的中点,AB=6cm,点D是线段AB上一点,且DB=1cm,求线段CD的长.
如图,点C是线段AB的中点,AB=6cm,点D是线段AB上一点,且DB=1cm,求线段CD的长.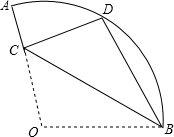 如图,在扇形OAB看,∠AOB=105°,将扇形OAB沿过点A的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OB于点C,且OC=2$\sqrt{2}$,则$\widehat{BD}$的长为$\frac{4}{3}$π.
如图,在扇形OAB看,∠AOB=105°,将扇形OAB沿过点A的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OB于点C,且OC=2$\sqrt{2}$,则$\widehat{BD}$的长为$\frac{4}{3}$π. 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边AC上一点O为圆心,OA为半径作圆,恰好经过边BC的中点D,并与边AC相交于另一点F.
如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边AC上一点O为圆心,OA为半径作圆,恰好经过边BC的中点D,并与边AC相交于另一点F.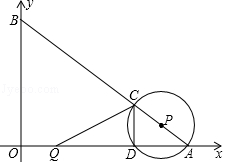 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.