题目内容
8.如图,半径为r的⊙O分别绕面积相等的等边三角形、正方形和圆用相同速度匀速滚动一周,用时分别为t1、t2、t3,则t1、t2、t3的大小关系为t1>t2>t3.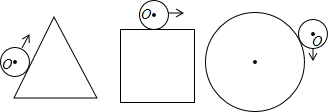
分析 根据面积,可得相应的周长,根据有理数的大小比较,可得答案.
解答 解:设面积相等的等边三角形、正方形和圆的面积为S,等边三角形、正方形的边长分别为a,b,圆的半径为r,
等边三角形的面积S=$\frac{\sqrt{3}}{4}$a2,周长=3a=3$\sqrt{\frac{4S}{\sqrt{3}}}$,
正方形的面积S=b2,周长=4b=4$\sqrt{S}$,
圆的面积S=πr2,周长=2πr=2π$\sqrt{\frac{S}{π}}$,
周长平方后的结果分别为12$\sqrt{3}$S,16S,4πS
∴t1>t2>t3.
故答案为:t1>t2>t3.
点评 本题考查了轨迹,利用相等的面积求出相应的周长是解题关键.

练习册系列答案
相关题目
19.据报道,滕州市某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水30万吨,将30万用科学记数法表示应为( )
| A. | 0.3×106 | B. | 3×105 | C. | 3×106 | D. | 30×104 |
13.某工厂现在平均每天比原计划多生产30台机器,现在生产500台机器所需时间与圆计划生产350台机器所需时间相同.设原计划平均每天生产x台机器,下面所列方程正确的是( )
| A. | $\frac{500}{x+30}=\frac{350}{x}$ | B. | $\frac{500}{x-30}=\frac{350}{x}$ | C. | $\frac{500}{x}=\frac{350}{x-30}$ | D. | $\frac{500}{x}=\frac{350}{x+30}$ |
18.下列图标既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°.
为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°. 如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=2,则k的值为6+2$\sqrt{5}$.
如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=2,则k的值为6+2$\sqrt{5}$.