题目内容
20. 如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=2,则k的值为6+2$\sqrt{5}$.
如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=2,则k的值为6+2$\sqrt{5}$.
分析 设E(x,x),则B(2,x+2),根据反比例函数系数的几何意义得出x2=2(x+2),求得E的坐标,从而求得k的值.
解答 解:设E(x,x),
∴B(2,x+2),
∵反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B、E.
∴x2=2(x+2),
解得x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$(舍去),
∴k=x2=6+2$\sqrt{5}$,
故答案为6+2$\sqrt{5}$.
点评 本题考查了反比例函数图象上点的坐标特征,关键是掌握反比例函数图象上点与反比例函数中系数k的关系.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
11. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+$\frac{1}{2}$∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;
②∠BOC=90°+$\frac{1}{2}$∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
5.如果x2-x-1=(x+1)0,那么x的值为( )
| A. | 2或-1 | B. | 0或1 | C. | 2 | D. | -1 |
9.九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 (x-60)元;②月销量是 (400-2x)件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
(1)请用含x的式子表示:①销售该运动服每件的利润是 (x-60)元;②月销量是 (400-2x)件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
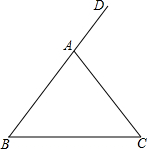 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角. 如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A,B两点.
如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A,B两点.