题目内容
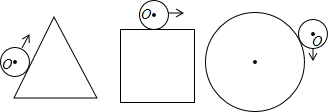
16. 为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°.
为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°.(Ⅰ)∠ACB的度数为96°;
(Ⅱ)求隧道AB的长.(参考数据:tan54°=1.4,$\sqrt{3}$=1.7,结果保留整数)
分析 (Ⅰ)由三角形内角和定理来解答;
(Ⅱ)首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD中,利用∠CAB的正切求得AD的长,继而求得答案.
解答  解:(Ⅰ)在△ABC中,∠CAB=54°,∠CBA=30°,则∠ACB=180°-54°-30°=96°.
解:(Ⅰ)在△ABC中,∠CAB=54°,∠CBA=30°,则∠ACB=180°-54°-30°=96°.
故答案是:96°;
(Ⅱ)过点C作CD⊥AB于D,
∵BC=200m,∠CBA=30°,
∴在Rt△BCD中,CD=$\frac{1}{2}$BC=100m,
BD=BC•cos30°=200×$\frac{\sqrt{3}}{2}$=100$\sqrt{3}$≈170(m).
∵∠CAB=54°,
∴在Rt△ACD中,AD=$\frac{CD}{tan∠CAB}$=$\frac{CD}{tan54°}$=$\frac{100}{1.4}$≈71(m).
∴AB=AD+BD≈170+71=241(m).
答:隧道AB的长约为241m.
点评 此题考查了解直角三角形的应用.此题难度适中,注意掌握辅助线的作法,注意把实际问题转化为数学问题求解.

练习册系列答案
相关题目
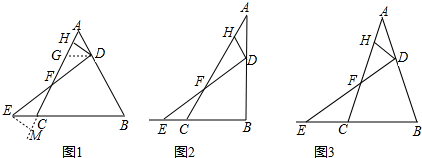
11. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+$\frac{1}{2}$∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;
②∠BOC=90°+$\frac{1}{2}$∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
5.如果x2-x-1=(x+1)0,那么x的值为( )
| A. | 2或-1 | B. | 0或1 | C. | 2 | D. | -1 |