题目内容
14.若函数y=$\frac{k}{x}$的图象过点(3,-2),那么它一定还经过点( )| A. | (3,2) | B. | (-3,-2) | C. | (2,-2) | D. | (-1,6) |
分析 分别计算各点的横纵坐标之积,然后根据反比例函数图象上点的坐标特征进行判断.
解答 解:∵函数y=$\frac{k}{x}$的图象过点(3,-2),
∴k=3×(-2)=-6,
而3×2=6,-3×(-2)=6,2×(-2)=-4,-1×6=-6,
∴点(-1,6)在反比例函数y=-$\frac{6}{x}$的图象上.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
2.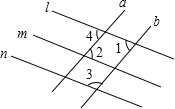 如图,下面说法正确的是( )
如图,下面说法正确的是( )
 如图,下面说法正确的是( )
如图,下面说法正确的是( )| A. | 如果∠1+∠3=180°,则l∥n | B. | 如果∠2=∠4,则a∥b | ||
| C. | 如果∠1=∠4,则l∥m | D. | 如果∠2=∠3,则m∥n |
19.在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD.如果再增加条件AC=BD,此四边形一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 都有可能 |
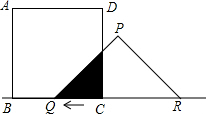 如图,有一边长为5的正方形ABCD和一等腰△PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线l上,当Q、C两点重合时,等腰△PQR以每秒1cm的速度沿直线l按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰△PQR重叠部分的面积为S.
如图,有一边长为5的正方形ABCD和一等腰△PQR,PQ=PR=5,QR=8,点B、Q、C、R在同一直线l上,当Q、C两点重合时,等腰△PQR以每秒1cm的速度沿直线l按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰△PQR重叠部分的面积为S. 如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.