题目内容
3.化简:(1)$\sqrt{24}$-($\sqrt{\frac{1}{2}}$+3$\sqrt{\frac{2}{3}}$)-($\sqrt{\frac{1}{8}}$-$\sqrt{6}$);
(2)a$\sqrt{\frac{1}{a}}$+$\sqrt{4b}$-($\frac{\sqrt{a}}{2}$-b$\sqrt{\frac{1}{b}}$)
分析 (1)、(2)先把各根式化为最减二次根式,再去括号,合并同类项即可.
解答 解:(1)原式=2$\sqrt{6}$-($\frac{\sqrt{2}}{2}$+$\sqrt{6}$)-($\frac{\sqrt{2}}{4}$-$\sqrt{6}$)
=2$\sqrt{6}$-$\frac{\sqrt{2}}{2}$-$\sqrt{6}$-$\frac{\sqrt{2}}{4}$+$\sqrt{6}$
=2$\sqrt{6}$-$\frac{3\sqrt{2}}{4}$;
(2)原式=$\sqrt{a}$+2$\sqrt{b}$-$\frac{\sqrt{a}}{2}$+$\sqrt{b}$
=$\frac{\sqrt{a}}{2}$+3$\sqrt{b}$.
点评 本题考查的是二次根式的加减,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
相关题目
14.若函数y=$\frac{k}{x}$的图象过点(3,-2),那么它一定还经过点( )
| A. | (3,2) | B. | (-3,-2) | C. | (2,-2) | D. | (-1,6) |
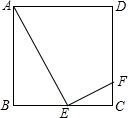 如图,正方形ABCD的边长为1,动点E在BC上,∠AEF=90°,EF交DC于F,当线段FC最长时,BE的长为$\frac{1}{2}$.
如图,正方形ABCD的边长为1,动点E在BC上,∠AEF=90°,EF交DC于F,当线段FC最长时,BE的长为$\frac{1}{2}$.