题目内容
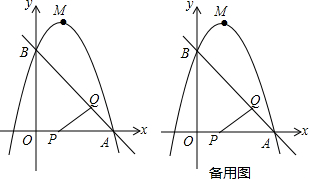
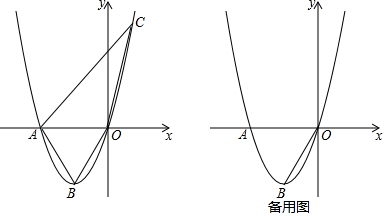
7.如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以$\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.(1)求抛物线的解析式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.
分析 (1)先求得直线AB与x轴、y轴的交点坐标,然后将点A、点B的坐标代入抛物线的解析式得到关于b、c的方程组求得b、c的值从而可得到抛物线的解析式;
(2)由点A、B的坐标可知OB=OA,从而可求得∠BAO=45°,然后分为∠PQA=90°和∠QPA=90°两种情况求解即可;
(3)由题意可知:EP∥FQ,EF∥PQ,故此四边形EFQP为平行四边形,从而得到PE=FQ,然后设点P的坐标为(t,0)则可表示出点Q、E、F的坐标,从而可求得PE、FQ的长,最后根据PE=FQ列方程求解即可.
解答 解:(1)∵y=-x+3与x轴交于点A,与y轴交于点B,
∴当y=0时,x=3,即A点坐标为(3,0),当x=0时,y=3,即B点坐标为(0,3).
∵将A(3,0),B(0,3)代入得:$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$.
∴抛物线的解析式为y=-x2+2x+3.
(2)∵OA=OB=3,∠BOA=90°,
∴∠QAP=45°.
如图①所示:∠PQA=90°时.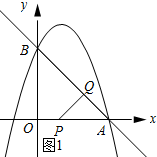
设运动时间为t秒,则QA=$\sqrt{2}$t,PA=3-t.
在Rt△PQA中,$\frac{QA}{PA}$=$\frac{\sqrt{2}}{2}$,即$\frac{\sqrt{2}t}{3-t}$=$\frac{\sqrt{2}}{2}$,
解得:t=1.
如图②所示:∠QPA=90°时.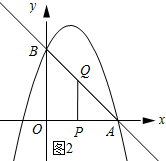
设运动时间为t秒,则QA=$\sqrt{2}$t,PA=3-t.
在Rt△PQA中,$\frac{PA}{AQ}$=$\frac{\sqrt{2}}{2}$,即$\frac{3-t}{\sqrt{2}t}$=$\frac{\sqrt{2}}{2}$,
解得:t=$\frac{3}{2}$.
综上所述,当t=1或t=$\frac{3}{2}$时,△PQA是直角三角形.
(3)如图③所示: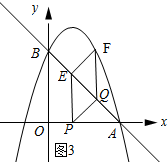
设点P的坐标为(t,0),则点E的坐标为(t,-t+3),
则EP=3-t.点Q的坐标为(3-t,t),点F的坐标为(3-t,-(3-t)2+2(3-t)+3),即F(3-t,4t-t2),
则FQ=4t-t2-t=3t-t2.
∵EP∥FQ,EF∥PQ,
∴四边形EFQP为平行四边形.
∴EP=FQ,即3-t=3t-t2.
解得:t1=1,t2=3(舍去).
将t=1代入得点F的坐标为(2,3).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了一次函数图象上的点的坐标与函数解析式之间的关系、待定系数法二次函数的解析式、等腰三角形三角形的性质和判定、平行四边形的判定,用含t的式子表示EP和FQ的长是解题的关键.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案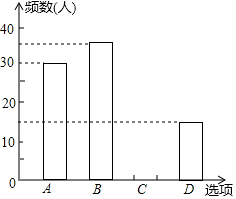 鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
鸡年春节前夕,海春中学向全校3000名学生发出“减少空气污染,少放烟花炮竹”倡议书,春节后随机抽取100名学生进行问卷调查,问卷选项有四项:A类:自己没有燃放烟花爆竹;B类:在规定的时间和规定的地点少放烟花爆竹;C类:随意燃放烟花爆竹;D类:不仅自己不燃放烟花爆竹同时劝阻身边亲友不燃放烟花爆竹,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:| 类别 | 频数 | 频率 |
| A | a | m |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | b | n |
| 合计 | 100 | 1.00 |
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“自己没有燃放放烟花爆竹”和“不仅自己不燃放同时劝阻身边亲友不燃放烟花爆竹”的学生共有多少名?
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
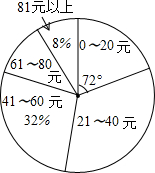 某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?
| 捐款 | 人数 |
| 0~20元 | |
| 21~40元 | |
| 41~60元 | |
| 61~80元 | 6 |
| 81元以上 | 4 |
| A. | 矩形的对角线相互垂直 | |
| B. | 顺次连结对角线相等的四边形各边中点所得到的四边形是矩形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |

| A. | 红红不是胜就是输,所以红红胜的概率为$\frac{1}{2}$ | |
| B. | 红红胜或娜娜胜的概率相等 | |
| C. | 两人出相同手势的概率为$\frac{1}{3}$ | |
| D. | 娜娜胜的概率和两人出相同手势的概率一样 |
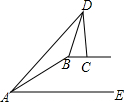 如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)
如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)