题目内容
13.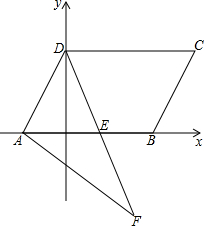 如图,平面直角坐标系中,点A、B均在x轴上,OA=2,OB=3,将线段AB向上平移3个单位,再向右平移2个单位,得到线段CD,连接AD、BC.
如图,平面直角坐标系中,点A、B均在x轴上,OA=2,OB=3,将线段AB向上平移3个单位,再向右平移2个单位,得到线段CD,连接AD、BC.(1)请写出C点的坐标;并求出四边形ABCD的面积;
(2)在y轴上是否存在点P,使S△PAD=S四边形ABDC?若存在,请写出点P的坐标;若不存在,请说明理由;
(3)如图:F是x轴下方位于线段AD右边的一个动点,连接DF、AF,DF交x轴于E,请猜测∠CDF、∠F、∠EAF之间的等量关系,并加以说明.
分析 (1)由OA=2,OB=3,可求得点B的坐标,又由将线段AB向上平移3个单位,再向右平移2个单位,得到线段CD,根据平移的性质,即可求得C点的坐标;继而求得四边形ABCD的面积;
(2)首先由S△PAD=S四边形ABDC,可求得$\frac{1}{2}$DP×2=15,继而求得DP=15,则可求得点P的坐标;
(3)由平行线的性质,可求得∠CDF=∠AED,然后又三角形外角的性质,证得∠CDF=∠F+∠EAF.
解答 解:(1)∵OA=2,OB=3,
∴点A(-2,0),点B(3,0),
∵将线段AB向上平移3个单位,再向右平移2个单位,得到线段CD,
∴点C(5,3),
∵AB∥CD,AB=CD,
∴四边形ABCD四平行四边形,
∴S四边形ABCD=5×3=15;
(2)存在.
则S△PAD=DP×2×$\frac{1}{2}$=DP,
∵S△PAD=S四边形ABDC=15,
∴DP=15,
∴点P(0,18)或(0,-12);
(3)∠CDF=∠F+∠EAF.
理由:∵AB∥CD,
∴∠CDF=∠AED,
∵∠AED=∠F+∠EAF,
∴∠CDF∠F+∠EAF.
点评 此题考查了平移的性质、平行线的性质以及三角形外角的性质.注意掌握平移中的对应关系.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
5.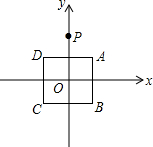 正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )
正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )
 正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )
正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )| A. | (0,2) | B. | (2,0) | C. | (0,-2) | D. | (-2,0) |
2. 如图是正方体的平面展开图,每个面上标有一个汉字,与“我”字相对的面上的字是( )
如图是正方体的平面展开图,每个面上标有一个汉字,与“我”字相对的面上的字是( )
 如图是正方体的平面展开图,每个面上标有一个汉字,与“我”字相对的面上的字是( )
如图是正方体的平面展开图,每个面上标有一个汉字,与“我”字相对的面上的字是( )| A. | 魅 | B. | 力 | C. | 绵 | D. | 阳 |

 我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?,题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是多少尺?
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?,题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是多少尺?
 如图,已知AB∥CD,∠BAE=40°,∠ECD=70°,EF平分∠AEC,则∠AEF的度数是55°.
如图,已知AB∥CD,∠BAE=40°,∠ECD=70°,EF平分∠AEC,则∠AEF的度数是55°.