��Ŀ����
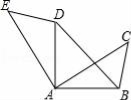
1����ͼ����֪����������ABC�У���BAC=30�㣬AB=AC����PAB=��������B����ֱ��AP�ĶԳƵ�Ϊ��D������AD������BD��AP�ڵ�G������CD��AP�ڵ�E����AB�ڵ�F����1����ͼ��1������=15��ʱ���ٰ�Ҫ��ͼ�Σ��������ACD�Ķ�������̽��DE��BF�ı�����ϵ������֤����
��2����ֱ��AP�Ƶ�A˳ʱ����ת�Ĺ����У�0�㣼a��75�㣩������AEFΪ����������ʱ��������ҳ����ͼֱ���������ֵΪ30���52.5�㣮
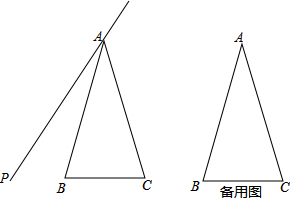
���� ��1���ٰ�Ҫ�����ɣ�
�ڸ��ݵ�B����ֱ��AP�ĶԳƵ�Ϊ��D���õ�AP��ֱƽ��BD�����ô�ֱƽ���ߵ����ʣ�֤����ACDΪ�ȱ������Σ����ɵõ���ACD=60�㣻
��DE=2BF������EB������AP��ֱƽ��BD���õ�ED=EB�����õȱ߶ԵȽǵõ���3=��4�����õ��������ε����������3=��4=15�㣬��5=30�㣬����ΪAD=AC��ABƽ�֡�DAC������AB��DC�����ɵõ�EB=2BF������ED=2BF��
��2������ͼ�Σ�������������ۣ���AE=AFʱ����AE=EFʱ����EF=AFʱ��
��� �⣺��1������ͼ1��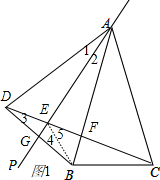
�ڡ�B��D����AP�Գƣ�
��AP��ֱƽ��BD��a=15�㣬
��AD=AB����1=��2=15�㣬
�ߡ�BAC=30�㣬
���DAC=��1+��2+��BAC=60�㣬
��AC=AB��
��AC=AD��
���ACDΪ�ȱ�������
���ACD=60�㣮
��DE=2BF��
֤��������EB��
��AP��ֱƽ��BD��
��ED=EB��
���3=��4��
��AB=AD����DAB=30�㣬
���ADB=75�㣬
�֡�ADC=60�㣬
���3=��4=15�㣬
���5=30�㣬
��AD=AC��ABƽ�֡�DAC��
��AB��DC��
��EB=2BF��
��ED=2BF��
��2����ͼ2��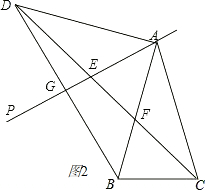
��AD=AC��
���DAC�ǵ���������
���ADC=��180��-2a-30�㣩��2=75��-a��
���AEF=��ADC+��DAE=75��-a+a=75�㣬
��AE=AFʱ����EAF=a=180��-75���2=180��-150��=30�㣻
��AE=EFʱ����EAF=a=��180��-75�㣩��=52.5�㣻
��EF=AFʱ����AEF=��EAF=a=75�㣨��ȥ����
�ʴ�Ϊ��30���52.5�㣮
���� ���⿼������ͼ���������Ĺؼ�������ͼ�Σ����ô�ֱƽ���ߵ����ʣ����������ε����ʣ��ȱ������ε����ʽ�����⣮


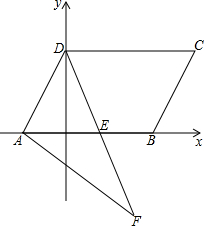 ��ͼ��ƽ��ֱ������ϵ�У���A��B����x���ϣ�OA=2��OB=3�����߶�AB����ƽ��3����λ��������ƽ��2����λ���õ��߶�CD������AD��BC��
��ͼ��ƽ��ֱ������ϵ�У���A��B����x���ϣ�OA=2��OB=3�����߶�AB����ƽ��3����λ��������ƽ��2����λ���õ��߶�CD������AD��BC��