题目内容
1.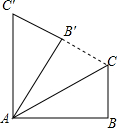 如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.
如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.
分析 根据旋转的性质可得AC′=AC,∠AB′C′=∠B,利用“HL”证明Rt△AB′C和Rt△AB′C′全等,根据全等三角形对应角相等可得∠B′AC=∠B′AC′,再根据两直线平行,同旁内角互补求出∠BAC′=90°,根据旋转的性质可得∠BAC=∠B′AC′,然后求解即可.
解答 解:∵△ABC绕点A旋转至△AB′C′的位置,
∴AC′=AC,∠AB′C′=∠B=90°,
在Rt△AB′C和Rt△AB′C′中,$\left\{\begin{array}{l}{AC=AC′}\\{AB′=AB′}\end{array}\right.$,
∴Rt△AB′C≌Rt△AB′C′(HL),
∴∠B′AC=∠B′AC′,
∵AC′∥BC,
∴∠BAC′=180°-∠B=180°-90°=90°,
∵△ABC绕点A旋转至△AB′C′的位置,
∴∠BAC=∠B′AC′,
∴∠BAC=∠B′AC=∠B′AC′,
∴∠BAC=90°÷3=30°.
故答案为:30°.
点评 本题考查了旋转的性质,全等三角形的判定与性质,平行线的性质,旋转前后对应角相等,对应边相等.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
16.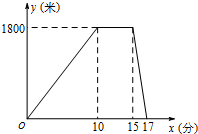 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )| A. | 小明在公园休息了15分钟 | B. | 小明乘出租车用了17分 | ||
| C. | 小明跑步的速度为120米/分 | D. | 出租车的平均速度是900米/分 |
6.研究表明,弹簧挂上物体后会伸长,已知弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是自变量的函数?
(2)当物体的质量为3kg时,弹簧的长度是多少?
(3)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(4)当物体的质量为3.5kg时,你能说出弹簧的长度吗?
(5)当弹簧的长度为12.5cm时,根据(3)求出所挂物体的质量.
| 物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | … |
| 弹簧的长度(cm) | 8 | 8.5 | 9 | 9.5 | 10 | … |
(2)当物体的质量为3kg时,弹簧的长度是多少?
(3)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(4)当物体的质量为3.5kg时,你能说出弹簧的长度吗?
(5)当弹簧的长度为12.5cm时,根据(3)求出所挂物体的质量.