题目内容
11.已知∠AOB=27°,∠AOC=$\frac{4}{5}$∠BOC,则∠AOC的度数为12°或108°.分析 通过分析,可知有两种情况:①OC在∠AOB的内部;②OC在∠AOB的外部,画图后分别计算即可.
解答 解:①OC在∠AOB的内部,如图,
∵∠AOB=27°,∠AOC=$\frac{4}{5}$∠BOC,
设∠BOC=x,则∠AOC=$\frac{4}{5}$x,
x$+\frac{4}{5}$x=27°,
x=15°,
$∠AOC=\frac{4}{5}$×15°=12°;
②OC在∠AOB的外部,如图,
∵∠AOB=27°,∠AOC=$\frac{4}{5}$∠BOC,
设∠BOC=x,则∠AOC=$\frac{4}{5}$x,
x$-\frac{4}{5}$x=27°,
x=135°,
$∠AOC=\frac{4}{5}$×135°=108°;
故答案为:12°或108°.
点评 本题考查了角的计算.解题的关键是注意画图,并分情况讨论.

练习册系列答案
相关题目
20.已知2x=3y(y≠0),则下面结论成立的是( )
| A. | $\frac{x}{y}$=$\frac{3}{2}$ | B. | $\frac{x}{3}$=$\frac{2}{y}$ | C. | $\frac{x}{y}$=$\frac{2}{3}$ | D. | $\frac{x}{2}$=$\frac{y}{3}$ |
19.已知反比例函数y=$\frac{k}{x}$的图象在第二、第四象限内,函数图象上有两点A(8,y1)、B(5,y2),则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
6. 如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )
如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )
 如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )
如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )| A. | 720° | B. | 360° | C. | 180° | D. | 540° |
20. 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )
 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )| A. | ∠1和∠4是同位角 | B. | ∠1和∠3是同位角 | ||
| C. | ∠1和∠2是同旁内角 | D. | ∠5和∠6是内错角 |
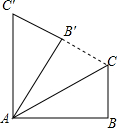 如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.
如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.