题目内容
13．已知△ABC为等边三角形，点O为△ABC的外心（三边中垂线的交点），若AB=2$\sqrt{3}$，则点O到BC边的距离为1．分析 如图，连接OB，作OH⊥BC于H．在Rt△OBH中，求出OH即可解决问题．
解答 解：如图，连接OB，作OH⊥BC于H．
∵△ABC是等边三角形，O是外心，
∴OB平分∠ABC，BH=HC=$\sqrt{3}$
∴∠OBH=$\frac{1}{2}$×60°=30°，
∴OH=BH•tan30°=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1，
∴点O到BC边的距离为1，
故答案为1．
点评 本题考查三角形的外心、等边三角形的性质．锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．
练习册系列答案
相关题目
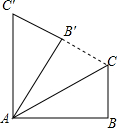如图，在△ABC中，∠B=90°，将△ABC绕点A旋转至△AB′C′的位置，若AC′∥BC，C′B′的延长线过点C，则∠BAC的度数为30°．
在如图的正方形网格中，每个小正方形的边长均为1个单位，将△ABC绕点C逆时针旋转90°，得到△A′B′C′；再将△A′B′C′，向右平移2个单位，得到△A″B″C″；请你画出△A′B′C′和△A″B″C″（不要求写画法）
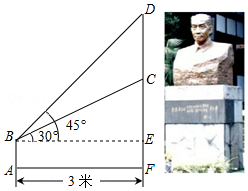如图，某学校在“国学经典”中新建了一座吴玉章雕塑，小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°，看雕塑底部C的仰角为30°，求塑像CD的高度．（最后结果精确到0.1米，参考数据：$\sqrt{3}$≈1.7）
如图，曲线l是由函数y=$\frac{6}{x}$在第一象限内的图象绕坐标原点O逆时针旋转45°得到的，过点A（-4$\sqrt{2}$，4$\sqrt{2}}$），B（2$\sqrt{2}$，2$\sqrt{2}}$）的直线与曲线l相交于点M、N，则△OMN的面积为8．