题目内容
1.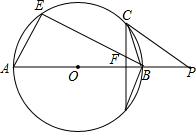 如图,AB为⊙O的直径,P是AB延长线上一点,CD是⊙O的弦,CD⊥AB,∠PCB=∠CDB,E是$\widehat{AC}$上的任一点,连接AE,BE,BE交弦CD于点F.
如图,AB为⊙O的直径,P是AB延长线上一点,CD是⊙O的弦,CD⊥AB,∠PCB=∠CDB,E是$\widehat{AC}$上的任一点,连接AE,BE,BE交弦CD于点F.(1)求证:PC是⊙O的切线;
(2)证明:BC2=BF•BE;
(3)若BE∥PC时,sin∠P=$\frac{3}{5}$,CF=5,求AE的长.
分析 (1)连接AC,OC,根据圆周角定理得到∠PCB=∠1,∠ACB=90°,于是得到∠1+∠OBC=90°,根据等腰三角形的性质得到∠OCB=∠OBC,于是得到∠PCB+∠OCB=90°即可得到结论;
(2)连接CE,根据圆周角定理得到∠3=∠2,推出△EBC∽△CBF,根据相似三角形的性质得到$\frac{BC}{BF}=\frac{BE}{BC}$,于是得到结论;
(3)根据平行线的性质得到OC⊥BE,∠5=∠P,等量代换得到$\widehat{EC}=\widehat{BD}$,于是得到∠2=∠4,解直角三角形即可得到结论.
解答 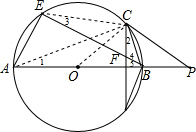 解:连接AC,OC,
解:连接AC,OC,
∵∠PCB=∠BDC,∠BDC=∠1,
∴∠PCB=∠1,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠1+∠OBC=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠PCB+∠OCB=90°,
即∠OCP=90°,
∴PC是⊙O的切线;
(2)连接CE,
∵AB⊥CD,AB为⊙O的直径,
∴$\widehat{BC}=\widehat{BD}$,
∴∠3=∠2,
∵∠4=∠4,
∴△EBC∽△CBF,
∴$\frac{BC}{BF}=\frac{BE}{BC}$,
∴BC2=BF•BE;
(3)∵BE∥PC,OC⊥PC,
∴OC⊥BE,∠5=∠P,
∴$\widehat{BE}=\widehat{BC}$,
∵$\widehat{BC}=\widehat{BD}$,
∴$\widehat{EC}=\widehat{BD}$,
∴∠2=∠4,
∴CF=BF=5,
∵sin∠5=sin∠p=$\frac{3}{5}$,
∴$\frac{FH}{5}=\frac{3}{5}$,
∴FH=3,
∴BH=$\sqrt{{5}^{2}-{3}^{2}}$=4,CH=5+3=8,
设⊙O的半径为r,
∵r2=(r-4)2+82,
∴r=10,
∵sin∠5=$\frac{AE}{AB}$,
∴$\frac{3}{5}=\frac{AE}{20}$,
∴AE=12.
点评 本题考查了切线的判定、相似三角形的判定与性质、圆周角定理、等腰三角形的性质、矩形的判定与性质、圆内接四边形的性质等知识;本题综合性强,有一定难度,证明三角形相似是解决问题的关键.

| A. | x≥-1 | B. | x≤-1 | C. | x≠-1 | D. | x>-1 |
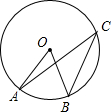 如图,点A、B、C在⊙O上,∠C+∠AOB=60°,则∠AOB的大小为( )
如图,点A、B、C在⊙O上,∠C+∠AOB=60°,则∠AOB的大小为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
 如图,AB∥CD,点E在直线CD上,EA平分∠CEB,若∠BED=40°,则∠A大小为( )
如图,AB∥CD,点E在直线CD上,EA平分∠CEB,若∠BED=40°,则∠A大小为( )| A. | 80° | B. | 70° | C. | 50° | D. | 40° |
| A. | -ab+1 | B. | -ab+b | C. | -a+1 | D. | -a-1 |
 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为2.
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为2.