题目内容
13. 在括号内空白处填写推理依据:
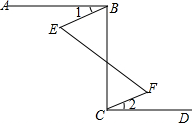
在括号内空白处填写推理依据:如图:AB⊥BC,BC⊥CD,∠1=∠2,∠E=62°,求∠F的度数.
解:∵AB⊥BC,BC⊥CD(已知)
∴∠ABC=90°,∠BCD=90°(垂直定义)
∵∠1=∠2(已知)
∴∠EBC=∠BCF(等式的性质)
∴EB∥CF(内错角相等,两直线平行)
∴∠F=∠E(两直线平行,内错角相等)
∵∠E=62°(已知)
∴∠F=62°(等量代换)
分析 根据垂直求出∠ABC=90°,∠BCD=90°,求出∠EBC=∠BCF,根据平行线的判定得出EB∥CF,根据平行线的性质得出∠F=∠E即可.
解答 解:∵AB⊥BC,BC⊥CD(已知),
∴∠ABC=90°,∠BCD=90°(垂直定义),
∵∠1=∠2(已知),
∴∠EBC=∠BCF(等式的性质),
∴EB∥CF(内错角相等,两直线平行),
∴∠F=∠E(两直线平行,内错角相等),
∵∠E=62°(已知),
∴∠F=62°(等量代换),
故答案为:垂直定义,等式的性质,内错角相等,两直线平行,两直线平行,内错角相等.
点评 本题考查了平行线的性质和判定,能综合运用定理进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.一元二次方程x2-4x+5=0的根的情况是( )
| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
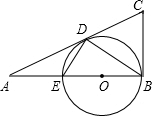 已知:如图,在Rt△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
已知:如图,在Rt△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.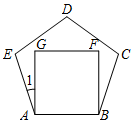 有一个正五边形和一个正方形边长相等,如图放置,则∠1=18°.
有一个正五边形和一个正方形边长相等,如图放置,则∠1=18°.



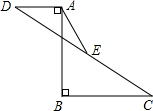 如图,AB⊥BC于点B,AB⊥AD于点A,AD=5,AB=12,BC=10,E是CD的中点,则AE的长是6.5.
如图,AB⊥BC于点B,AB⊥AD于点A,AD=5,AB=12,BC=10,E是CD的中点,则AE的长是6.5.