题目内容
二次函数y=ax2+bx+c(a≠0)的图象如图,以下结论正确的是( )


| A、abc>0 |
| B、方程ax2+bx+c=0有两个实数根分别为-2和6 |
| C、a-b+c<0 |
| D、当y=4时,x的取值只能为0 |
考点:二次函数图象与系数的关系,抛物线与x轴的交点
专题:
分析:A、根据抛物线的开口方向、与y轴的交点坐标及抛物线的对称轴即可判定;
B、根据抛物线与x轴的交点的横坐标即可判定;
C、当x=-1时,y=a-b+c,然后结合图象即可判定;
D、根据抛物线的对称性和图象即可判定.
B、根据抛物线与x轴的交点的横坐标即可判定;
C、当x=-1时,y=a-b+c,然后结合图象即可判定;
D、根据抛物线的对称性和图象即可判定.
解答:解:A、根据图象知道:a<0,c>0,对称轴在y轴的右边,∴b>0,∴abc<0,故选项错误;
B、∵抛物线与x轴的交点的横坐标为-2和6,∴方程ax2+bx+c=0有两个实数根分别为-2和6,故选项正确;
C、∵当x=-1时,y=a-b+c,而根据图象知道当x=-1时函数值y>0,∴a-b+c>0,故选项错误;
D、∵抛物线是轴对称图形,当y=4时,有两个对应的自变量的取值,故选项错误.
故选B.
B、∵抛物线与x轴的交点的横坐标为-2和6,∴方程ax2+bx+c=0有两个实数根分别为-2和6,故选项正确;
C、∵当x=-1时,y=a-b+c,而根据图象知道当x=-1时函数值y>0,∴a-b+c>0,故选项错误;
D、∵抛物线是轴对称图形,当y=4时,有两个对应的自变量的取值,故选项错误.
故选B.
点评:此题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
若四个互不相等的正实数a,b,c,d满足(a2012-c2012)(a2012-d2012)=2012,(b2012-c2012)(b2012-d2012)=2012,则(ab)2012-(cd)2012的值为( )
| A、-2012 | B、-2011 |
| C、2012 | D、2011 |
 由若干个相同小正方体组合成一个几何体,使组合几何体的主视图、俯视图如图所示.这样的组合几何体不只有一种,它的组成最少需要x个小正方体,最多需要y个小正方体.则y-x的值为( )
由若干个相同小正方体组合成一个几何体,使组合几何体的主视图、俯视图如图所示.这样的组合几何体不只有一种,它的组成最少需要x个小正方体,最多需要y个小正方体.则y-x的值为( )| A、4 | B、3 | C、2 | D、1 |
若a+b=2012,b≠a+1,则
的值等于( )
| a2-b2+2b-1 |
| a2-b2+a+b |
| A、2012 | ||
| B、2011 | ||
C、
| ||
D、
|
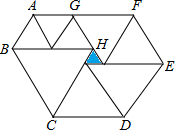 如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为1cm,现欲将此图案的周边镶上一根彩线,问彩线至少需要多长?
如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为1cm,现欲将此图案的周边镶上一根彩线,问彩线至少需要多长?



 如图,共6个同样的小正方体码放在5乘5的方格纸上,则正视图
如图,共6个同样的小正方体码放在5乘5的方格纸上,则正视图