题目内容
15．已知菱形的两条对角线长分别是6cm和8cm，则菱形的边长是（ ）| A． | 5cm | B． | 7cm | C． | 10cm | D． | 12cm |
分析 根据菱形的性质求得OD，OA的长，再根据勾股定理求得边长AD的长．
解答 解：如图：∵菱形ABCD中BD=6cm，AC=8cm，
∴OD=
$\frac{1}{2}$BD=3cm，OA=$\frac{1}{2}$AC=4cm，
在直角三角形AOD中AD=$\sqrt{D{O}^{2}+A{O}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5cm．
故选A．
点评 此题主要考查学生对菱形的性质及勾股定理的理解及运用，关键是掌握菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．
练习册系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
5．下列函数：①y=2x2+x+1 ②y=3x+1 ③y=x（x-2）-x2 ④y=-x中，是一次函数的有（ ）个．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
3．在数轴上表示不等式x+6≥2的解集，正确的是（ ）
| A． |  | B． |  | C． |  | D． |  |
10．
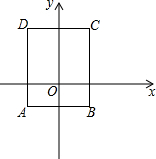如图，四边形ABCD是长方形，AB=3，AD=4．已知A（-$\frac{3}{2}$，-1），则点C的坐标是（ ）
如图，四边形ABCD是长方形，AB=3，AD=4．已知A（-$\frac{3}{2}$，-1），则点C的坐标是（ ）| A． | （-3，$\frac{3}{2}$） | B． | （$\frac{3}{2}$，-3） | C． | （3，$\frac{3}{2}$） | D． | （$\frac{3}{2}$，3） |
如图，已知A（-2，2），B（-3，-2），C（3，-2）把△ABC向上平移4个单位长度，再向右平移2个单位得到△A1B1C1，解答下列各题：
如图，在?ABCD中，AE⊥BC，垂足为E，如果AB=5，AE=4，BC=8，有下列结论：