题目内容
6.如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE.
(1)若AB=18,BC=21,求DE的长;
(2)若AB=a,求DE的长(用含a的代数式表示)
分析 (1)根据线段的和差,可得BD的长,AE的长,再由线段的和差,可得答案;
(2)根据线段的和差,可得BD、AE的长,再根据线段的和差,可得DE=$\frac{2}{3}$AB.
解答 解:(1)由线段的和差,得
AC=AB+BC=18+21=39,BC=CD+BD=2BD+BD=21.
解得BD=7.
由线段的和差,得
AC=AE+CE=AE+2AE=3AE=39,
解得AE=13.
由线段的和差,得
BE=AB-AE=18-13=5,
DE=BE+BD=5+7=12;
(2)由线段的和差,得CD+BD=BC,即2BD+BD=BC,
BD=$\frac{1}{3}$BC.
由线段的和差,得CE+AE=AC,即2AE+AE=AC,
AE=$\frac{1}{3}$AC.
由线段的和差,得
BE=AB-AE=AB-$\frac{1}{3}$AC.
DE=BE+BD=AB-$\frac{1}{3}$AC+$\frac{1}{3}$BC=AB-$\frac{1}{3}$(AC-BC)=AB-$\frac{1}{3}$AB=$\frac{2}{3}$AB,
∵AB=a,
∴DE=$\frac{2}{3}$a.
点评 本题考查了两点间的距离,利用线段的和差得出BD、AE的长是解题关键.

练习册系列答案
相关题目
18.某校准备选出甲、乙两人中的一人参加县里的射击比赛,他们在相同条件下各射靶5次,成绩统计如下:
(1)求甲、乙两人射击成绩的方差分别是多少?
(2)已知该校选手前三年都取得了县射击比赛的第一名,请问应选择谁去参加比赛?
| 命中环数/环 | 7 | 8 | 9 | 10 |
| 甲命中的频数/次 | 1 | 1 | 0 | 3 |
| 乙命中的频数/次 | 0 | 1 | 3 | 1 |
(2)已知该校选手前三年都取得了县射击比赛的第一名,请问应选择谁去参加比赛?
 如图,射线OM上有三点A、B、C,满足OA=60cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以1cm/秒的速度匀速运动.
如图,射线OM上有三点A、B、C,满足OA=60cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以1cm/秒的速度匀速运动. 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.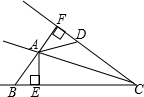 如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.
如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.