题目内容
1. 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果保留根号)
分析 (1)延长PQ交直线AB于点E,根据直角三角形两锐角互余求得即可;
(2)设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
解答 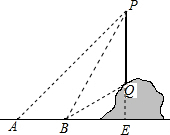 解:延长PQ交直线AB于点E,如图所示:
解:延长PQ交直线AB于点E,如图所示:
(1)∠BPQ=90°-60°=30°;
(2)设PE=x米.
在直角△APE中,∠A=45°,
则AE=PE=x米;
∵∠PBE=60°,
∴∠BPE=30°,
在直角△BPE中,BE=$\frac{\sqrt{3}}{3}$PE=$\frac{\sqrt{3}}{3}$x米,
∵AB=AE-BE=9米,
则x-$\frac{\sqrt{3}}{3}$x=9,
解得:x=$\frac{27+9\sqrt{3}}{2}$.
则BE=$\frac{9\sqrt{3}+9}{2}$米.
在直角△BEQ中,QE=$\frac{\sqrt{3}}{3}$BE=$\frac{9+3\sqrt{3}}{2}$米.
∴PQ=PE-QE=$\frac{27+9\sqrt{3}}{2}$-$\frac{9+3\sqrt{3}}{2}$=9+3$\sqrt{3}$(米).
答:电线杆PQ的高度为(9+3$\sqrt{3}$)米.
点评 本题考查了仰角的定义、解直角三角形、三角函数;运用三角函数求出PE和QE是解决问题的关键.

练习册系列答案
相关题目
9.在比例尺是1:46000的城市交通游览图上,某条道路的图上距离长约8cm,则这条道路的实际长度约为( )
| A. | 368×103cm | B. | 36.8×104cm | C. | 3.68×105cm | D. | 3.68×106cm |
10.下列艺术字是轴对称图形的是( )
| A. | 理 | B. | 想 | C. | 高 | D. | 中 |
17.一个直角三角形的三边分别是6cm、8cm、xcm,则x=( )cm.
| A. | 100cm | B. | 10cm | C. | 10cm或2$\sqrt{7}$cm | D. | 100cm或28cm |
 如图:AOB为直线,OC平分∠AOD,∠BOD=42°,则∠AOC=69°.
如图:AOB为直线,OC平分∠AOD,∠BOD=42°,则∠AOC=69°. 如图,在△ABC中,CD是AB边上高,若AD=16,CD=12,BD=9.
如图,在△ABC中,CD是AB边上高,若AD=16,CD=12,BD=9.
 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).