题目内容
19.解方程x4-6x2+5=0这是一个一元四次方程,根据该方程的特点,我们通常可以这样来解:设x2=y,那么x4=y2,于是原方程可变为y2-6y+5=0…①,解这个方程得:y1=1,y2=5.当y=1时,x2=1,∴x=±1;当y=5时,x2=5,∴x=±$\sqrt{5}$.所以原方程有四个根:x1=1,x2=-1,x3=$\sqrt{5}$,x4=-$\sqrt{5}$.(1)这一解法在由原方程得到方程①的过程中,利用了换元法达到降次的目的,体现了转化的数学思想.
(2)参照上面解题的思想方法解方程:($\frac{x}{{x}^{2}-1}$)2-$\frac{5x}{{x}^{2}-1}$+6=0.
分析 (1)用一个字母表示一个较复杂的代数式的方法叫换元法.
(2)用y代替$\frac{x}{{x}^{2}-1}$,然后解关于y的一元二次方程,求得y的值后,再来求关于x的分式方程,注意要验根.
解答 解:(1)在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了转化的数学思想.
故答案是:换元;转化;
(2)设y=$\frac{x}{{x}^{2}-1}$,则由原方程得到:y2-5y+6=0,
整理,得
(y-3)(y-2)=0,
解得y=3或y=2.
当y=3时,$\frac{x}{{x}^{2}-1}$=3,即3x2-x-3=0,则x=$\frac{1±\sqrt{37}}{6}$,解得x1=$\frac{1+\sqrt{37}}{6}$,x2=$\frac{1-\sqrt{37}}{6}$,
经检验,它们都是原方程的根;
当y=2时,$\frac{x}{{x}^{2}-1}$=2,即2x2-x-2=0,则x=$\frac{1±\sqrt{17}}{4}$,解得x3=$\frac{1+\sqrt{17}}{4}$,x4=$\frac{1-\sqrt{17}}{4}$,
经检验,它们都是原方程的根;
综上所述,原方程的根为:x1=$\frac{1+\sqrt{37}}{6}$,x2=$\frac{1-\sqrt{37}}{6}$,x3=$\frac{1+\sqrt{17}}{4}$,x4=$\frac{1-\sqrt{17}}{4}$.
点评 本题主要考查了换元法,即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.

练习册系列答案
相关题目
14. 如图,在△ABC中,AB=6$\sqrt{5}$,AC=12,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P、Q,则线段PQ长度的最小值是( )
如图,在△ABC中,AB=6$\sqrt{5}$,AC=12,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P、Q,则线段PQ长度的最小值是( )
 如图,在△ABC中,AB=6$\sqrt{5}$,AC=12,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P、Q,则线段PQ长度的最小值是( )
如图,在△ABC中,AB=6$\sqrt{5}$,AC=12,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P、Q,则线段PQ长度的最小值是( )| A. | 6 | B. | 12 | C. | $\frac{12\sqrt{5}}{5}$ | D. | 6$\sqrt{5}$ |
11. 如图,?ABCD中,E是BC边的中点,已知△BEF的面积为S,则△ABF的面积为( )
如图,?ABCD中,E是BC边的中点,已知△BEF的面积为S,则△ABF的面积为( )
 如图,?ABCD中,E是BC边的中点,已知△BEF的面积为S,则△ABF的面积为( )
如图,?ABCD中,E是BC边的中点,已知△BEF的面积为S,则△ABF的面积为( )| A. | S | B. | 2S | C. | 3S | D. | 4S |
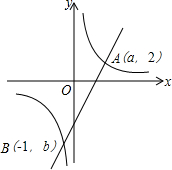 如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3.
如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3. 如图,在四边形ABCD中,AD∥BC,过点A作AE∥DC交BC于点E,BD平分∠ABC,求证:AB=EC.
如图,在四边形ABCD中,AD∥BC,过点A作AE∥DC交BC于点E,BD平分∠ABC,求证:AB=EC. 如图,在?ABCD中,∠ABC的平分线交AD于点E,交CD的延长线于点F,
如图,在?ABCD中,∠ABC的平分线交AD于点E,交CD的延长线于点F,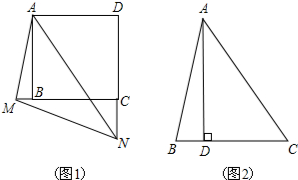
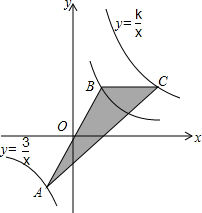 如图,点A在双曲线y=$\frac{3}{x}$第三象限的分支上,连结AO并延长交第一象限的图象于点B,画BC∥x轴交反比例函数y=$\frac{k}{x}$的图象于点C,若△ABC的面积为6,则k的值是9.
如图,点A在双曲线y=$\frac{3}{x}$第三象限的分支上,连结AO并延长交第一象限的图象于点B,画BC∥x轴交反比例函数y=$\frac{k}{x}$的图象于点C,若△ABC的面积为6,则k的值是9.