题目内容
19.计算:(1)${({π-1})^0}-{({-\frac{1}{2}})^{-1}}-{2^2}$
(2)(x+y)2(x-y)2
(3)$\frac{2012}{{{{2012}^2}-2013×2011}}$
(4)先化简,再求值:(3x+2)(3x-2)-5x(x-1)-(2x-1)2,其中$x=-\frac{1}{3}$.
分析 (1)先算0指数幂、负整数指数幂与乘方,再算减法;
(2)利用平方差公式和完全平方公式计算;
(3)把2013×2011利用平方差公式计算,再进一步计算化简即可;
(3)利用平方差公式、完全平方公式和整式的乘法计算方法计算,进一步合并化简,最后代入求得数值即可.
解答 解:(1)原式=1-(-2)-4
=1+2-4
=-1;
(2)原式=(x2-y2)2
=x4-2x2y2+y4;
(3)原式=$\frac{2012}{201{2}^{2}-(2012+1)(2012-1)}$
=$\frac{2012}{201{2}^{2}-201{2}^{2}+1}$
=2012;
(4)原式=9x2-4-5x2+5x-4x2+4x-1
=4x-5.
点评 此题考查整式的混合运算与化简求值,掌握计算公式和计算方法是解决问题的关键.

练习册系列答案
相关题目
11.一个DNA分子的直径约为0.0000002cm,用科学记数法表示为( )
| A. | 0.2×10-6cm | B. | 2×10-6cm | C. | 0.2×10-7cm | D. | 2×10-7cm |
8.一个多边形的每一个外角都是72°,那么这个多边形的内角和为( )
| A. | 540° | B. | 720° | C. | 900° | D. | 1080° |
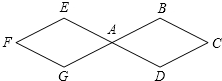 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.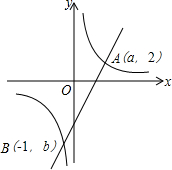 如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3.
如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3.