Question

20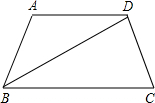．如图，在四边形ABCD中，AD∥BC，BD平分∠ABC，∠A=2∠ABC，∠C=∠ABC．
（1）求∠ADB的度数；
（2）求证：BD⊥CD．

Answer 1

分析 （1）根据平行线的性质得到∠A+∠ABC=180°，根据已知条件得到∠A=120°，∠ABC=60°，根据角平分线的定义得到∠ABD=∠DBC=30°，根据平行线的性质即可得到结论；
（2）根据（1）的结论和已知条件即可得到结论．

解答 解：（1）∵AD∥BC，
∴∠A+∠ABC=180°，
∵∠A=2∠ABC，
∴∠A=120°，∠ABC=60°，
∵BD平分∠ABC，
∴∠ABD=∠DBC=30°，
∵AD∥BC，
∴∠ADB=∠DBC=30°；

（2）∵∠C=∠ABC=60°，
∵∠DBC=30°，
∴∠BDC=90°，
∴BD⊥CD．

点评 本题考查直角三角形30°角所对的直角边等于斜边的一半的性质，平行线的性质，三角形的内角和定理，熟记性质并求出△BCD是直角三角形是解题的关键．