题目内容
9.先阅读理解下列例题,再按要求完成作业.例题:解一元二次不等式(3x-6)(2x+4)>0.
由有理数的乘法法则“两数相乘,同号得正”有①$\left\{\begin{array}{l}{3x-6>0}\\{2x+4>0}\end{array}\right.$或②$\left\{\begin{array}{l}{3x-6<0}\\{2x+4<0}\end{array}\right.$.
解不等式组①得x>2,解不等式组②得x<-2.
所以一元二次不等式(3x-6)(2x+4)>0的解集是x>2或x<-2.
(1)求不等式(2x+8)(3-x)<0的解集;
(2)求不等式$\frac{5x+15}{4-2x}$>0的解集.
分析 (1)由有理数的乘法法则“两数相乘,异号得负”得出两个不等式组,求出每个不等式组的解集即可;
(2)由有理数的除法法则“两数相除,同号得正”得出两个不等式组,求出每个不等式组的解集即可.
解答 解:(1)由有理数的乘法法则“两数相乘,异号得负”
有①$\left\{\begin{array}{l}{2x+8>0}\\{3-x<0}\end{array}\right.$或②$\left\{\begin{array}{l}{2x+8<0}\\{3-x>0}\end{array}\right.$,
解不等式组①得x>3,
解不等式组②得x<-4,
所以一元二次不等式(2x+8)(3-x)<0的解集是x>3或x<-4;
(2)由有理数的除法法则“两数相除,同号得正”
有①$\left\{\begin{array}{l}{5x+15>0}\\{4-2x>0}\end{array}\right.$或②$\left\{\begin{array}{l}{5x+15<0}\\{4-2x<0}\end{array}\right.$,
解不等式组①得:-3<x<2,
解不等式组②无解,
所以不等式$\frac{5x+15}{4-2x}$>0的解集是-3<x<2.
点评 本题考查了解一元一次不等式组的应用,能根据题意得出两个不等式组是解此题的关键.

练习册系列答案
相关题目
18.为了解某市八年级学生的课外数学阅读的时间,从中随机调查了400名学生的课外数学阅读的时间.下列说法正确的是( )
| A. | 某市八年级学生是总体 | |
| B. | 每一名八年级学生是个体 | |
| C. | 400名八年级学生是总体的一个样本 | |
| D. | 样本容量是400 |
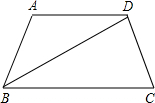 如图,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=2∠ABC,∠C=∠ABC.
如图,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=2∠ABC,∠C=∠ABC.
 已知一次函数与反比例函数的图象交于点P(-2,1)和Q(1,m),如图是在同一直角坐标系中这两个函数图象的示意图,观察图象并回答:
已知一次函数与反比例函数的图象交于点P(-2,1)和Q(1,m),如图是在同一直角坐标系中这两个函数图象的示意图,观察图象并回答: