题目内容
对于线段的中点,有以下几种说法:①若AM=MB,则M是AB的中点;②若AM=MB=
AB,则M是AB的中点;③若AM=
AB,则M是AB的中点;④若A,M,B在一条直线上,且AM=MB,则M是AV的中点.其中正确的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、①④ | B、②④ |
| C、①②④ | D、①②③④ |
考点:直线、射线、线段
专题:
分析:利用数形结合方法即可判定.
解答:解:①若AM=MB,则M是AB的中点;错误,因为点A,B,M要在一条直线上,
②若AM=MB=
AB,则M是AB的中点;正确,
③若AM=
AB,则M是AB的中点;错误,
④若A,M,B在一条直线上,且AM=MB,则M是AM的中点.正确.
所以正确的有②④.
故选:B.
②若AM=MB=
| 1 |
| 2 |
③若AM=
| 1 |
| 2 |
④若A,M,B在一条直线上,且AM=MB,则M是AM的中点.正确.
所以正确的有②④.
故选:B.
点评:本题主要考查了线段的中点,解题的关键是数形结合.

练习册系列答案
相关题目
四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AC=BD;②AC⊥BD;③AC与BD互相平分;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则下列推理成立的是( )
| A、①④?⑥ | B、②④?⑥ |
| C、①②?⑥ | D、①③?⑤ |
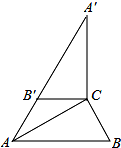 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )A、4
| ||
| B、6 | ||
C、3
| ||
| D、3 |
已知锐角α,且sinα=cos37°,则α等于( )
| A、37° | B、63° |
| C、53° | D、45° |
函数y=ax2+a与y=
(a≠0)在同一坐标系中可能的图象为( )
| a |
| x |
A、 |
B、 |
C、 |
D、 |
 如图,直线AB、CD、EF都经过点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=
如图,直线AB、CD、EF都经过点O,且AB⊥CD,OG平分∠BOE,如果∠EOG= 如图为二次函数y=ax2+bx+c(a≠0)的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=-1,x2=3;③a+b+c>0;④当x>1时,y随x的增大而增大;⑤2a-b=0,正确的说法有
如图为二次函数y=ax2+bx+c(a≠0)的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=-1,x2=3;③a+b+c>0;④当x>1时,y随x的增大而增大;⑤2a-b=0,正确的说法有 将一副直角三角形ABC和DEF如图所示(其中∠A=60°,∠F=45°),使点E落在AC边上,且ED∥BC,求∠CEF的度数.
将一副直角三角形ABC和DEF如图所示(其中∠A=60°,∠F=45°),使点E落在AC边上,且ED∥BC,求∠CEF的度数.