题目内容
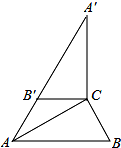 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )A、4
| ||
| B、6 | ||
C、3
| ||
| D、3 |
考点:旋转的性质
专题:计算题
分析:先利用互余计算出∠BAC=30°,再根据含30度的直角三角形三边的关系得到AB=2BC=4,接着根据旋转的性质得A′B′=AB=4,B′C=BC=2,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,于是可判断△CAA′为等腰三角形,所以∠CAA′=∠A′=30°,再利用三角形外角性质计算出∠B′CA=30°,可得B′A=B′C=2,然后利用AA′=AB′+A′B′进行计算.
解答:解:∵∠ACB=90°,∠B=60°,
∴∠BAC=30°,
∴AB=2BC=2×2=4,
∵△ABC绕点C顺时针旋转得到△A′B′C′,
∴A′B′=AB=4,B′C=BC=2,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,
∴△CAA′为等腰三角形,
∴∠CAA′=∠A′=30°,
∵A、B′、A′在同一条直线上,
∴∠A′B′C=∠B′AC+∠B′CA,
∴∠B′CA=60°-30°=30°,
∴B′A=B′C=2,
∴AA′=AB′+A′B′=2+4=6.
故选B.
∴∠BAC=30°,
∴AB=2BC=2×2=4,
∵△ABC绕点C顺时针旋转得到△A′B′C′,
∴A′B′=AB=4,B′C=BC=2,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,
∴△CAA′为等腰三角形,
∴∠CAA′=∠A′=30°,
∵A、B′、A′在同一条直线上,
∴∠A′B′C=∠B′AC+∠B′CA,
∴∠B′CA=60°-30°=30°,
∴B′A=B′C=2,
∴AA′=AB′+A′B′=2+4=6.
故选B.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
如果阳光斜射在地面上,一张矩形纸片在地面上的影子不可能是( )
| A、矩形 | B、线段 |
| C、平行四边形 | D、一个点 |
对于线段的中点,有以下几种说法:①若AM=MB,则M是AB的中点;②若AM=MB=
AB,则M是AB的中点;③若AM=
AB,则M是AB的中点;④若A,M,B在一条直线上,且AM=MB,则M是AV的中点.其中正确的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、①④ | B、②④ |
| C、①②④ | D、①②③④ |
已知抛物线y=x2-2x+c与y轴的交点为(0,1),下列说法不正确的是( )
| A、抛物线开口向上 |
| B、抛物线与x轴的交点为(1,0) |
| C、当x=1时,y的最大值为0 |
| D、当x>1时,y的值随着x的值增大而增大 |
 如图所示,已知∠AOC=40°,∠BOD=50°,OM,ON分别是∠AOC,∠BOD的角平分线,则∠MON=
如图所示,已知∠AOC=40°,∠BOD=50°,OM,ON分别是∠AOC,∠BOD的角平分线,则∠MON= 如图,已知长方形OABC,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0).
如图,已知长方形OABC,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0).