题目内容
 将一副直角三角形ABC和DEF如图所示(其中∠A=60°,∠F=45°),使点E落在AC边上,且ED∥BC,求∠CEF的度数.
将一副直角三角形ABC和DEF如图所示(其中∠A=60°,∠F=45°),使点E落在AC边上,且ED∥BC,求∠CEF的度数.考点:平行线的性质
专题:
分析:根据直角三角形两锐角互余求出∠1,再根据两直线平行,内错角相等求出∠2,然后根据∠CEF=45°-∠2计算即可得解.
解答: 解:∵∠A=60°,∠F=45°,
解:∵∠A=60°,∠F=45°,
∴∠1=90°-60°=30°,∠DEF=90°-45°=45°,
∵ED∥BC,
∴∠2=∠1=30°,
则∠CEF=∠DEF-∠2=45°-30°=15°.
 解:∵∠A=60°,∠F=45°,
解:∵∠A=60°,∠F=45°,∴∠1=90°-60°=30°,∠DEF=90°-45°=45°,
∵ED∥BC,
∴∠2=∠1=30°,
则∠CEF=∠DEF-∠2=45°-30°=15°.
点评:本题考查了平行线的性质,直角三角形两锐角互余的性质是基础题,熟记性质是解题的关键.

练习册系列答案
相关题目
对于线段的中点,有以下几种说法:①若AM=MB,则M是AB的中点;②若AM=MB=
AB,则M是AB的中点;③若AM=
AB,则M是AB的中点;④若A,M,B在一条直线上,且AM=MB,则M是AV的中点.其中正确的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、①④ | B、②④ |
| C、①②④ | D、①②③④ |
 如图几何体的主视图是( )
如图几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
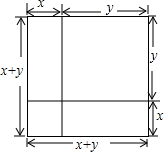 仔细观察图形,依据图形面积间的关系,不添加辅助线,便可得到一个熟悉的公式,这个公式是( )
仔细观察图形,依据图形面积间的关系,不添加辅助线,便可得到一个熟悉的公式,这个公式是( )| A、(x-y)2=x2-xy+y2 |
| B、(x-y)2=x2-2xy+y2 |
| C、(x+y)2=x2+2xy+y2 |
| D、(x+y)2=x2+y2 |
 如图,已知长方形OABC,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0).
如图,已知长方形OABC,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0).