题目内容
 如图,直线AB、CD、EF都经过点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=
如图,直线AB、CD、EF都经过点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=| 1 |
| 4 |
考点:对顶角、邻补角,垂线
专题:
分析:根据角平分线,可得∠BOG,根据角的和差,可得关于∠EOG的方程,根据余角的性质,可得∠COE的度数,根据对顶角的性质,可得∠DOF的度数,根据角的和差,可得答案.
解答:解:由OG平分∠BOE,得∠BOG=∠EOG,
由∠EOG=
∠AOE,得4∠EOG=∠AOE,
由角的和差,得∠AOE+∠EOG+∠BOG=180°,即4∠EOG+∠EOG+∠EOG=180°,
解得∠EOG=30°,
由角的和差,得∠COE=90°-∠BOE=90°-60°=30°,
由对顶角相等,得∠DOF=30°,
由角的和差,得∠AOF=90°-∠DOF=90°-30°=60°.
由∠EOG=
| 1 |
| 4 |
由角的和差,得∠AOE+∠EOG+∠BOG=180°,即4∠EOG+∠EOG+∠EOG=180°,
解得∠EOG=30°,
由角的和差,得∠COE=90°-∠BOE=90°-60°=30°,
由对顶角相等,得∠DOF=30°,
由角的和差,得∠AOF=90°-∠DOF=90°-30°=60°.
点评:本题考查了对顶角、邻补角,利用了角平分线的性质,角的和差,对顶角相等.

练习册系列答案
相关题目
若a+b+c=0,则
+
+
+
+
+
+
的值为( )
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
| |ab| |
| ab |
| |ac| |
| ac |
| |bc| |
| bc |
| |abc| |
| abc |
| A、-7 | B、-1 | C、1 | D、7 |
如果阳光斜射在地面上,一张矩形纸片在地面上的影子不可能是( )
| A、矩形 | B、线段 |
| C、平行四边形 | D、一个点 |
对于线段的中点,有以下几种说法:①若AM=MB,则M是AB的中点;②若AM=MB=
AB,则M是AB的中点;③若AM=
AB,则M是AB的中点;④若A,M,B在一条直线上,且AM=MB,则M是AV的中点.其中正确的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、①④ | B、②④ |
| C、①②④ | D、①②③④ |
一个有50个数据的样本,落在某一小组内的频率是0.3,在这50个数据中,落在这一小组内的频数是( )
| A、50 | B、30 | C、15 | D、3 |
 如图,△ABC中,点D在线段AB上,且∠BAD=∠C,则下列结论一定正确的是( )
如图,△ABC中,点D在线段AB上,且∠BAD=∠C,则下列结论一定正确的是( )| A、AB2=AC•BD |
| B、AB•AD=BD•BC |
| C、AB2=BC•BD |
| D、AB•AD=BD•CD |
 如图几何体的主视图是( )
如图几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
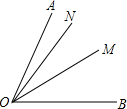 (1)如图,∠AOB的平分线为OM,0N为∠AOM内的一条射线,若∠BON=57°,∠AON=11°时,求∠MON的度数;
(1)如图,∠AOB的平分线为OM,0N为∠AOM内的一条射线,若∠BON=57°,∠AON=11°时,求∠MON的度数;