题目内容
某市在道路改造过程中，需要铺设一条为2000米的管道，决定由甲、乙两个工程队来完成这一工程，已知甲工程队比乙工程队每天能多铺设20米，且甲工程队铺设600米所用的天数与乙工程队铺设500米所用的天数相同，甲、乙工程队每天各能铺设多少米？
考点：分式方程的应用
专题：
分析：设乙工程队每天铺设x米，则甲工程队每天铺设（x+20）米，根据甲工程队铺设600米所用的天数与乙工程队铺设500米所用的天数相同建立方程求出其解即可
解答：解：设乙工程队每天铺设x米，则甲工程队每天铺设（x+20）米，由题意，得
=
，
解得：x=100．
经检验，x=100是原方程的解．
则甲工程队每天铺设100+20=120米．
答：乙工程队每天铺设100米，则甲工程队每天铺设120米．
| 600 |
| x+20 |
| 500 |
| x |
解得：x=100．
经检验，x=100是原方程的解．
则甲工程队每天铺设100+20=120米．
答：乙工程队每天铺设100米，则甲工程队每天铺设120米．
点评：本题考查了列分式方程解实际问题的运用，分式方程的解法的运用，工程问题的数量关系工作总量÷工作效率=工作时间的运用，解答时根据甲工程队铺设600米所用的天数与乙工程队铺设500米所用的天数相同建立方程是关键．
练习册系列答案
名题金卷系列答案
相关题目
已知一个二次函数y=ax2+bx+c的图象经过A（若a+b+c=0，则
+
+
+
+
+
+
的值为（ ）
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
| |ab| |
| ab |
| |ac| |
| ac |
| |bc| |
| bc |
| |abc| |
| abc |
| A、-7 | B、-1 | C、1 | D、7 |
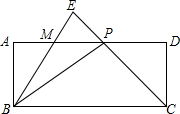已知在矩形ABCD中，P是边AD上的一动点，联结BP、CP，过点B作射线交线段CP的延长线于点E，交边AD于点M，且使得∠ABE=∠CBP，如果AB=2，BC=5，AP=x，PM=y；