题目内容
7.用一根长60cm的铁丝围成一个矩形,那么矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为( )| A. | y=x2-30x(0<x<30) | B. | y=-x2+30x(0≤x<30) | C. | y=-x2+30x(0<x<30) | D. | y=-x2+30x(0<x≤30) |
分析 由矩形另一边长为周长的一半减去已知边长求得另一边的长,进一步根据矩形的面积等于相邻两边长的积列出关系式即可.
解答 解:由题意得:矩形的另一边长=60÷2-x=30-x,
矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为y=x(30-x)=-x2+30x(0<x<30).
故选:C.
点评 此题主要考查了根据实际问题列二次函数关系式;掌握矩形的边长与所给周长与另一边长的关系是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,AB∥CD,∠2=2∠1,则∠3=( )
如图,AB∥CD,∠2=2∠1,则∠3=( )
 如图,AB∥CD,∠2=2∠1,则∠3=( )
如图,AB∥CD,∠2=2∠1,则∠3=( )| A. | 50° | B. | 60° | C. | 65° | D. | 70° |
19.在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
| A. | 扩大100倍 | B. | 缩小100倍 | C. | 不变 | D. | 不能确定 |
17.某公司根据市场计划调整投资策略,对A、B两种产品进行市场调查,收集数据如下表:
其中,m是待定系数,其值是由生产A的材料的市场价格决定的,变化范围是6<m<8,销售B产品时需缴纳$\frac{1}{20}$x2万元的关税.其中,x为生产产品的件数.假定所有产品都能在当年售出,设生产A,B两种产品的年利润分别为y1、y2(万元).
(1)写出y1、y2与x之间的函数关系式,注明其自变量x的取值范围.
(2)请你通过计算比较,该公司生产哪一种产品可使最大年利润更大?
| 项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
| A | 20 | m | 10 | 200 |
| B | 40 | 8 | 18 | 120 |
(1)写出y1、y2与x之间的函数关系式,注明其自变量x的取值范围.
(2)请你通过计算比较,该公司生产哪一种产品可使最大年利润更大?
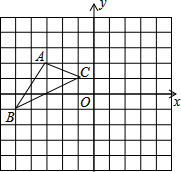 如图,在平面直角坐标系中,△ABC的顶点A的坐标是(-3,2).
如图,在平面直角坐标系中,△ABC的顶点A的坐标是(-3,2). 一个物体由几个相同的正方体堆叠成,从三个不同方向观察得到的图形如图所示,试回答下面的问题:
一个物体由几个相同的正方体堆叠成,从三个不同方向观察得到的图形如图所示,试回答下面的问题: