题目内容
17.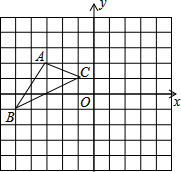 如图,在平面直角坐标系中,△ABC的顶点A的坐标是(-3,2).
如图,在平面直角坐标系中,△ABC的顶点A的坐标是(-3,2).(1)将△ABC先向右平移5个单位,再向上平移2个单位得到△A1B1C1,画出平移后的△A1B1C1;
(2)把△ABC绕点(1,1)逆时针旋转90°得到△A2B2C2,请画出△A2B2C2,并直接写出点A2、B2、C2的坐标为A2(0,-3),B2(3,-5),C2(1,-1);
(3)在这两次变换中,点A所经过的总路径的长为7+$\frac{\sqrt{17}}{2}$π单位.(结果保留根号和π)
分析 (1)利用点平移的规律些出点A、B、C的对应点A1、B1、C1的坐标,然后描点可得到△A1B1C1;
(2)利用网格特点和旋转的性质,画出点A、B、C的对应点A2、B2、C2,原式可得到△A2B2C2,再写出点A2、B2、C2的坐标;
(3)平移的距离为7,再利用弧长公式计算出由A旋转到A2的路径长,然后把两者相加即可.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,A2(0,-3),B2(3,-5),C2(1,-1);
(3)点A所经过的总路径的长=5+2+$\frac{90•π•\sqrt{17}}{180}$=7+$\frac{\sqrt{17}}{2}$π.
故答案为A2(0,-3),B2(3,-5),C2(1,-1),7+$\frac{\sqrt{17}}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
8.一次函数y=-x+3与x轴的交点是( )
| A. | $(\frac{1}{3},0)$ | B. | $(-\frac{1}{3},0)$ | C. | (3,0) | D. | (-3,0) |
2.给x位学生分配宿舍,x正好是12的倍数.如果每间宿舍住4人,最后多余1间宿舍;如果每间宿舍住3人,最后还缺2间,求学生人数.可列方程( )
| A. | $\frac{x-1}{4}$=$\frac{x+2}{3}$ | B. | $\frac{x}{4}$+1=$\frac{x}{3}$-2 | C. | 4(x-1)=3(x+2) | D. | $\frac{x}{4}$-1=$\frac{x}{3}$+2 |
7.用一根长60cm的铁丝围成一个矩形,那么矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为( )
| A. | y=x2-30x(0<x<30) | B. | y=-x2+30x(0≤x<30) | C. | y=-x2+30x(0<x<30) | D. | y=-x2+30x(0<x≤30) |
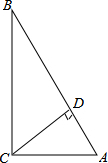 在△ABC中,∠C=90°,解这个直角三角形.
在△ABC中,∠C=90°,解这个直角三角形.