题目内容
2.如图1为抛物线桥洞,已知底面宽AB=16m,与拱顶M的距离4m.(1)在图2中,建立适当的坐标系,求抛物线的解析式;
(2)若水深1米,求水面CD的宽度(结果用根号表示)
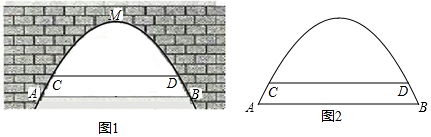
分析 (1)建立合适的坐标系,设出抛物线的解析式,由图中点在抛物线上,用待定系数法求出抛物线解析式;
(2)求出y=1时x的值即可得.
解答 解:(1)建立如图所示的坐标系,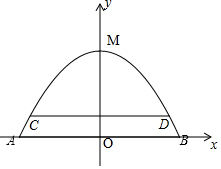
设这条抛物线的解析式为y=ax2+4(a≠0).由已知抛物线经过点B(8,0),
可得0=a×82+4,有a=-$\frac{1}{16}$,
∴抛物线的解析式为y=-$\frac{1}{16}$x2+4.
(2)当y=1时,1=-$\frac{1}{16}$x2+4,
解得:x=±4$\sqrt{3}$,
4$\sqrt{3}$-(-4$\sqrt{3}$)=8$\sqrt{3}$,
∴水面CD的宽为8$\sqrt{3}$m.
点评 本题主要考查了用待定系数法求二次函数的解析式,根据图中信息得出函数经过的点的坐标是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 如图,已知AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG的度数.
如图,已知AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG的度数.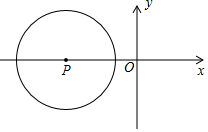 如图,在平面直角坐标系中,半径为2的圆P的圆心P的坐标为(-3,0),将圆P沿x轴的正方向平移,使得圆P与y轴相切,则平移的距离为( )
如图,在平面直角坐标系中,半径为2的圆P的圆心P的坐标为(-3,0),将圆P沿x轴的正方向平移,使得圆P与y轴相切,则平移的距离为( )
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).