题目内容
4．
如图，某中学准备围建一个矩形苗圃，其中一边靠墙，另外三边用长为30米的篱笆围成，若墙长为18米，设这个苗圃垂直于墙的一边长为x米．（1）若苗圃园的面积为100平方米，求x的值；
（2）若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值，如果没有，请说明理由．
分析 （1）根据矩形的面积公式列出关于x的方程，解方程可得答案；
（2）列出矩形的面积y关于x的函数解析式，结合x的取值范围，利用二次函数的性质可得最值情况．
解答 解：（1）由题意，得：平行于墙的一边长为（30-2x），
根据题意，得：x（30-2x）=100，
解得：x=5或x=15，
∵$\left\{\begin{array}{l}{30-2x≤18}\\{2x＜30}\end{array}\right.$
∴6≤x＜15．
∴x=10．
（2）∵矩形的面积y=x（30-2x）=-2（x-$\frac{15}{2}$）2+$\frac{225}{2}$，且30-2x≥8，即x≤11，
∴当x=7.5时，y取得最大值，最大值为$\frac{225}{2}$；
当x=11时，y取得最小值，最小值为88．
点评 本题考查了二次函数的应用、长方形的周长公式的运用、长方形的面积公式的运用、一元二次方程的解法的运用，解答时根据长方形的面积公式建立方程和函数解析式是关键．
练习册系列答案
相关题目
15．
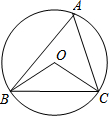如图，⊙O的半径为2，△ABC是⊙O的内接三角形，连结OB，OC，若∠BAC与∠BOC互补，则弦BC的长为（ ）
如图，⊙O的半径为2，△ABC是⊙O的内接三角形，连结OB，OC，若∠BAC与∠BOC互补，则弦BC的长为（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 2$\sqrt{2}$ | D． | 4 |
如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为1的等边三角形，点A在x轴上，点O，B1，B2，B3，…都在直线l上，则点A2的坐标是（2，$\sqrt{3}$），点A2017的坐标是（$\frac{2019}{2}$，$\frac{2017\sqrt{3}}{2}$）．
9．
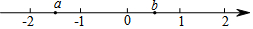实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）
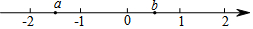实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）| A． | a+b＞0 | B． | a-b＞0 | C． | $\frac{a}{b}$＞0 | D． | b2＜a2 |
16．若直角三角形的两条直角边长分别是6和8，则它的外接圆半径为（ ）
| A． | $\sqrt{7}$ | B． | 4 | C． | 5 | D． | 10 |
14．若单项式x2ym-n与单项式-$\frac{1}{2}{x^{2m+n}}{y^3}$是同类项，那么这两个多项式的和是（ ）
| A． | $\frac{1}{2}{x^4}{y^6}$ | B． | $\frac{1}{2}{x^2}{y^3}$ | C． | $\frac{3}{2}{x^2}{y^3}$ | D． | $-\frac{1}{2}{x^2}{y^3}$ |