题目内容
4.如图①,在△ABC中,∠BAC=90°,AD⊥BC,垂足为点D,点M为AB上的动点,连接DM,过点D作DN⊥DM交AC于点N.当tanB=1时,DM=DN;若设tanB=$\frac{a}{b}$,如图②,那么DM与DN的数量关系为( )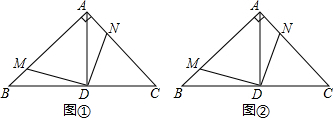
| A. | DM=DN | B. | DM=$\frac{a}{b}$DN | C. | DM=$\frac{b}{a}$DN | D. | DM=2DN |
分析 由△BDM∽△ADN得$\frac{BD}{AD}$=$\frac{DM}{DN}$,再根据tanB=$\frac{a}{b}$=$\frac{AD}{BD}$得$\frac{DN}{DM}$=$\frac{a}{b}$即可解决问题.
解答 解:如图②中,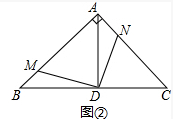 ∵AD⊥BC,MD⊥DN,
∵AD⊥BC,MD⊥DN,
∴∠MDN=∠BAD=90°,
∴∠BDM=∠ADN,
∵∠B+∠C=90°,∠C+∠DAC=90°,
∴∠B=∠DAN,
∴△BDM∽△ADN,
∴$\frac{BD}{AD}$=$\frac{DM}{DN}$,
∵tanB=$\frac{a}{b}$=$\frac{AD}{BC}$,
∴$\frac{DN}{DM}$=$\frac{a}{b}$,
∴DM=$\frac{b}{a}DN$,
故选C.
点评 本题考查相似三角形的判定和性质、锐角三角函数的定义的等知识解题的关键是正确寻找相似三角形,;于相似三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
14.如果x2+kx+81是一个两数和的平方,那么k的值是( )
| A. | 9 | B. | -9 | C. | 9或者-9 | D. | 18或者-18 |
9.在今年的“希望工程”捐款活动中,某班级一小组7名同学积极捐出自己的零花锇,奉献自己的爱心,他们捐款的数额分别是(单位:元)5O、20、5O、30、25、50、55,这组数据的众数和中位数分别是( )
| A. | 50元,30元 | B. | 50元,40元 | C. | 50元,50元 | D. | 55元,50元 |
16.下列各图中,∠1与∠2是对顶角的是( )
| A. | 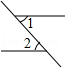 | B. |  | C. | 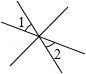 | D. | 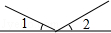 |
14.若关于x的一元二次方程(a+1)x2+x-a2+1=0有一个根为0,则a的值等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 1或者-1 |