题目内容
13.方程$\frac{x}{x-1}$-1=1的解是x=2.分析 根据等式的性质,可得整式方程,根据解整式方程,可得答案.
解答 解:两边都乘以(x-1),得
x-(x-1)=x-1,
解得x=2,
经检验:x=2是原分式方程的解,
故答案为:x=2.
点评 本题考查了分式方程的解,利用等式的性质转化成整式方程是解题关键,要检验分式方程的根.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.如图①,在△ABC中,∠BAC=90°,AD⊥BC,垂足为点D,点M为AB上的动点,连接DM,过点D作DN⊥DM交AC于点N.当tanB=1时,DM=DN;若设tanB=$\frac{a}{b}$,如图②,那么DM与DN的数量关系为( )
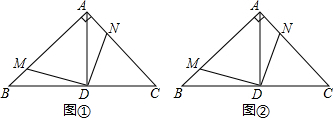

| A. | DM=DN | B. | DM=$\frac{a}{b}$DN | C. | DM=$\frac{b}{a}$DN | D. | DM=2DN |
18.下列代数式:①$\frac{2}{x}$,②$\frac{x+y}{5}$,③$\frac{1}{2-a}$,$\frac{x}{3}+\frac{3}{x}$.其中是分式的有( )
| A. | ①②③ | B. | ①②③④ | C. | ①③④ | D. | ①②④ |
3.某超市计划购进甲、乙两种品牌的新型节能台灯20盏,这两种台灯的进价和售价如下表所示:
设购进甲种台灯x盏,且所购进的两种台灯都能全部卖出.
(1)若该超市购进这批台灯共用去1000元,问这两种台灯购进多少盏?
(2)若购进两种台灯的总费用不超过1100元,那么超市如何进货才能获得最大利润?最大利润是多少?
(3)最终超市按照(2)中的方案进货,但实际销售中,由于乙品牌的台灯销售前景不容乐观,超市计划对乙品牌台灯进行降价销售,当毎盏台灯最多降价10元时,全部销售后才能使利润不低于550元.
| 甲 | 乙 | |
| 进价(元/件) | 40 | 60 |
| 售价(元/件) | 60 | 100 |
(1)若该超市购进这批台灯共用去1000元,问这两种台灯购进多少盏?
(2)若购进两种台灯的总费用不超过1100元,那么超市如何进货才能获得最大利润?最大利润是多少?
(3)最终超市按照(2)中的方案进货,但实际销售中,由于乙品牌的台灯销售前景不容乐观,超市计划对乙品牌台灯进行降价销售,当毎盏台灯最多降价10元时,全部销售后才能使利润不低于550元.
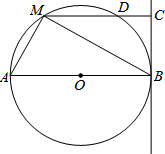 如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).
如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12). 如图是一个正方体的展开图,折叠成正方体后与“中”字相对的一面上的字是顺.
如图是一个正方体的展开图,折叠成正方体后与“中”字相对的一面上的字是顺. 有一道作业题:解方程$\frac{2x-1}{3}$=1-$\frac{x+2}{4}$.下面的纸片上是小明的解答过程:
有一道作业题:解方程$\frac{2x-1}{3}$=1-$\frac{x+2}{4}$.下面的纸片上是小明的解答过程: