题目内容
19.先化简,再求值:$({\frac{x}{x-2}-1})•\frac{{{x^2}-4}}{x-3}$,其中x=4.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{x-x+2}{x-2}$•$\frac{(x+2)(x-2)}{x-3}$
=$\frac{2}{x-2}$•$\frac{(x+2)(x-2)}{x-3}$
=$\frac{2(x+2)}{x-3}$,
当x=4时,原式=$\frac{2(4+2)}{4-3}$=12.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
9.下列语句中,是对顶角的语句为( )
| A. | 有公共顶点并且相等的两个角 | |
| B. | 两条直线相交,有公共顶点的两个角 | |
| C. | 顶点相对的两个角 | |
| D. | 两条直线相交,有公共顶点没有公共边的两个角 |
4.如图①,在△ABC中,∠BAC=90°,AD⊥BC,垂足为点D,点M为AB上的动点,连接DM,过点D作DN⊥DM交AC于点N.当tanB=1时,DM=DN;若设tanB=$\frac{a}{b}$,如图②,那么DM与DN的数量关系为( )
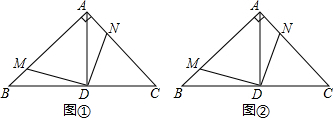

| A. | DM=DN | B. | DM=$\frac{a}{b}$DN | C. | DM=$\frac{b}{a}$DN | D. | DM=2DN |
11.将分式$\frac{3ab}{a-b}$中的a、b都扩大到3倍,则分式的值( )
| A. | 不变 | B. | 扩大3倍 | C. | 扩大9倍 | D. | 扩大6倍 |
 如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到△ABC,若BD=1,则AD的长为$\sqrt{3}$.
如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到△ABC,若BD=1,则AD的长为$\sqrt{3}$. 直线l1∥l2,一块含45°角的直角三角尺如图所示放置,∠1=85°,则∠2=130°.
直线l1∥l2,一块含45°角的直角三角尺如图所示放置,∠1=85°,则∠2=130°. 如图是一个正方体的展开图,折叠成正方体后与“中”字相对的一面上的字是顺.
如图是一个正方体的展开图,折叠成正方体后与“中”字相对的一面上的字是顺.