题目内容
4.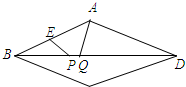 如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )
如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )| A. | 16 | B. | 21 | C. | 7+$\sqrt{85}$ | D. | 7+$\sqrt{61}$ |
分析 将菱形ABCD放置在平面直角坐标系中,使得B为原点,BD在x的正半轴上,根据题意得出A、B、E三点的坐标,将A平行向左移动2个单位到A'点,作A'关于x轴的对称点F,则F(6,-6),连EF,交x轴于点P,在x轴上向正方向上截取PQ=2,此时四边形AEPQ的周长最小,AQ+EP=A'P+EP=FP+EP=EF,由此即可得出结论.
解答 解:如图所示:
将菱形ABCD放置在平面直角坐标系中,使得B为原点,BD在x的正半轴上,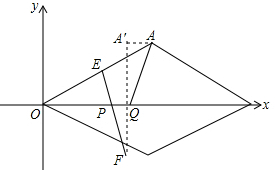
∵菱形ABCD的边长是10,对角线BD=16,点E是AB的中点,
∴A(8,6),B(0,0),E(4,3),将A平行向左移动2个单位到A'点,则A'(6,6),作A'关于x轴的对称点F,则F(6,-6),连EF,交x轴于点P,在x轴上向正方向上截取PQ=2,
此时,四边形AEPQ的周长最小,
∵AE=$\frac{AB}{2}$=5,PQ=2,AQ+EP=A'P+EP=FP+EP=EF,
四边形四边形AEPQ的周长=5+2+$\sqrt{(4-6)^{2}+(3+6)^{2}}$=7+$\sqrt{85}$.
故选C.
点评 本题考查的是轴对称-最短路线问题,根据题意作出辅助线是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列说法正确的是( )
| A. | 有且只有一条直线与已知直线平行 | |
| B. | 垂直于同一条直线的两条直线互相平行 | |
| C. | 从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 | |
| D. | 在平面内过一点有且只有一条直线与已知直线垂直 |
15.下列计算正确的是( )
| A. | am•a2=a2m | B. | (a3)2=a3 | ||
| C. | x3•x2•x=x5 | D. | a3n-5÷a5-n=a4n-10 |
9.如图是由边长为2的三个菱形组成的伸缩衣架,每个菱形的内角变化范围是60°到120°,则伸缩衣架的长度l的变化范围是( )


| A. | 2≤l≤2$\sqrt{3}$ | B. | 3≤l≤3$\sqrt{3}$ | C. | 3$\sqrt{3}$≤l≤6$\sqrt{3}$ | D. | 6$≤l≤6\sqrt{3}$ |
16.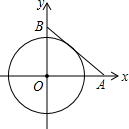 如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )
如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )
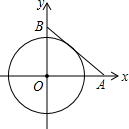 如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )
如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )| A. | 100π | B. | 25π | C. | 22π | D. | 20π |
14.将点A(3,-1)先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )
| A. | (6,1) | B. | (0,-3) | C. | (0,1) | D. | (6,-3) |
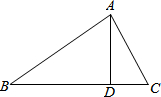 如图,点D在线段BC上,已知∠BAC=90°,∠DAC+∠C=90°,则∠BAD和∠C的大小关系是∠BAD=∠C,其依据是同角的余角相等.
如图,点D在线段BC上,已知∠BAC=90°,∠DAC+∠C=90°,则∠BAD和∠C的大小关系是∠BAD=∠C,其依据是同角的余角相等.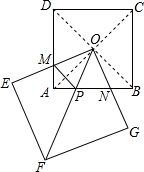 如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.
如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.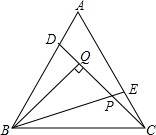 如图,点D,E分别是等边△ABC的两边AB,AC上的点,且AD=CE,BQ⊥CD于点Q,PQ=1,求BQ的长.
如图,点D,E分别是等边△ABC的两边AB,AC上的点,且AD=CE,BQ⊥CD于点Q,PQ=1,求BQ的长.