题目内容
17. 如图,矩形ABCD的周长是16,DE=2,△FEC是等腰三角形,∠FEC=90°,则AE的长是( )
如图,矩形ABCD的周长是16,DE=2,△FEC是等腰三角形,∠FEC=90°,则AE的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 设AE=x,由矩形的性质得出AB=CD,AD=BC=x+2,∠A=∠D=90°,得出CD=6-x,由已知条件得出EF=CE,∠DEC+∠AEF=90°,证出∠AFE=∠DEC,由AAS证明△AEF≌△DCE,得出AE=CD,即x=6-x,解方程即可.
解答 解:设AE=x,
∵四边形ABCD是矩形,
∴AB=CD,AD=BC=x+2,∠A=∠D=90°,
∴∠AFE+∠AEF=90°,
∵矩形ABCD的周长是16,
∴CD=AB=$\frac{1}{2}$(16-2x-4)=6-x,
∵△FEC是等腰三角形,∠FEC=90°,
∴EF=CE,∠DEC+∠AEF=90°,
∴∠AFE=∠DEC,
在△AEF和△DCE中,$\left\{\begin{array}{l}{∠A=∠D}&{\;}\\{∠AFE=∠DEC}&{\;}\\{EF=CE}&{\;}\end{array}\right.$,
∴△AEF≌△DCE(AAS),
∴AE=CD,
即x=6-x,
解得:x=3,
∴AE=3;
故选:A.
点评 本题考查了矩形的性质、全等三角形的判定与性质、等腰三角形的性质;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
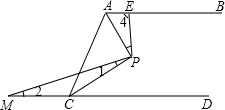 如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过P点作PM、PE交CD于M,交AB于E
如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过P点作PM、PE交CD于M,交AB于E