题目内容
9．若a＞b＞m＞0，求证：$\frac{b-m}{a-m}$＜$\frac{b}{a}$＜$\frac{b+m}{a+m}$．分析 由已知不等式判断得到b-a与a-m的正负，利用作差法比较即可．
解答 解：∵a＞b＞m＞0，
∴b-a＜0，a-m＞0，
∴$\frac{b-m}{a-m}$-$\frac{b}{a}$=$\frac{ab-am-ab+bm}{a（a-m）}$=$\frac{m（b-a）}{a（a-m）}$＜0，$\frac{b}{a}$-$\frac{b+m}{a+m}$=$\frac{ab+bm-ab-am}{a（a+m）}$=$\frac{m（b-a）}{a（a+m）}$＜0，
则$\frac{b-m}{a-m}$＜$\frac{b}{a}$＜$\frac{b+m}{a+m}$．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
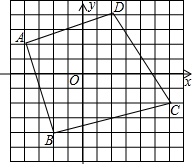已知，如图，四边形ABCD的顶点坐标分别为A（-4，2），B（-2，-4），C（6，-2），D（2，4），试以O点为位似中心作四边形A′B′C′D′，使四边形ABCD与四边形A′B′C′D′的位似比为2：1（只画一种情况）．
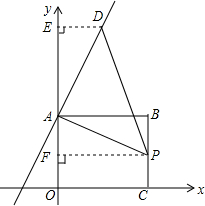如图，矩形ABCO位于直角坐标系平面，O为原点，A、C分别在坐标轴上，B的坐标为（8，5），线段BC上有一动点P，已知点D在第一象限
如图，矩形ABCD的周长是16，DE=2，△FEC是等腰三角形，∠FEC=90°，则AE的长是（ ）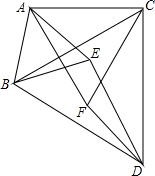
如图，以△ABC的各边为边，在BC的同一侧作等边三角形DBC，等边三角形ABE，等边三角形△ACF．