题目内容
6.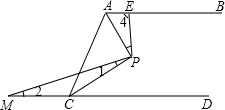 如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过P点作PM、PE交CD于M,交AB于E
如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过P点作PM、PE交CD于M,交AB于E(1)求证:PA⊥PC;
(2)当E、M在AB、CD上运动时,求∠3+∠4-∠1-∠2的值.
分析 (1)根据平行线的性质由AB∥CD得到∠BAC+∠DCA=90°,再根据角平分线的定义得到∠PAC=$\frac{1}{2}$∠BAC,∠PCA=$\frac{1}{2}$∠DCA,则∠PAC+∠PCA=90°,所以∠APC=90°;
(2)作PQ∥AB,根据平行线性质得到PQ∥CD,则∠APQ=180°-∠3-∠4,∠5=∠2,由于∠APQ+∠5+∠1=90°,则180°-∠3-∠4+∠2+∠1=90°,整理得到∠3+∠4-∠1-∠2=90°.
解答 (1)证明:∵AB∥CD,
∴∠BAC+∠DCA=90°,
∵PA平分∠BAC,PC平分∠ACD,
∴∠PAC=$\frac{1}{2}$∠BAC,∠PCA=$\frac{1}{2}$∠DCA,
∴∠PAC+∠PCA=$\frac{1}{2}$(∠BAC+∠DCA)=90°,
∴∠APC=90°,
∴PA⊥PC;
(2)解:②∠3+∠4-∠1-∠2不变正确.理由如下:作PQ∥AB,如图,
∵AB∥CD,
∴PQ∥CD,
由AB∥PQ得∠APQ+∠3+∠4=180°,即∠APQ=180°-∠3-∠4,
由PQ∥CD得∠5=∠2,
∵∠APQ+∠5+∠1=90°,
∴180°-∠3-∠4+∠2+∠1=90°,
∴∠3+∠4-∠1-∠2=90°.
点评 本题考查了角平分线的性质,平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
16. 如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是( )
如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是( )
 如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是( )
如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是( )| A. | PM>PN | B. | PM<PN | C. | PM=PN | D. | 不能确定 |
 如图,矩形ABCD的周长是16,DE=2,△FEC是等腰三角形,∠FEC=90°,则AE的长是( )
如图,矩形ABCD的周长是16,DE=2,△FEC是等腰三角形,∠FEC=90°,则AE的长是( )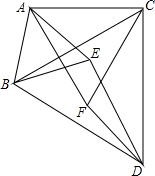 如图,以△ABC的各边为边,在BC的同一侧作等边三角形DBC,等边三角形ABE,等边三角形△ACF.
如图,以△ABC的各边为边,在BC的同一侧作等边三角形DBC,等边三角形ABE,等边三角形△ACF.