题目内容
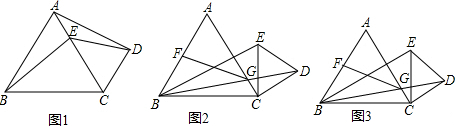
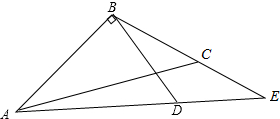
16. 如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°,∠A=40°.
如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°,∠A=40°.(1)试证明∠B=∠ADG;
(2)求∠B的度数.
分析 (1)由垂直可证明CD∥EF,进一步可证明DG∥BC,可得到∠B=∠ADG;
(2)在△ADG中由三角形内角和定理可求得∠ADG,结合(1)可求得∠B.
解答 (1)证明:∵CD⊥AB,EF⊥AB,
∴∠CDE=∠FEB=90°,
∴CD∥EF,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DG∥BC,
∴∠B=∠ADG;
(2)解:在△ADG中,∠3=80°,∠A=40°,
∴∠ADG=180°-∠A-∠3=180°-80°-40°=60°,
由(1)可知∠B=∠ADG,
∴∠B=60°.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
5.若a是最小的自然数,b是最大的负整数,c是倒数等于它本身的数,则a+b+c=( )
| A. | 0 | B. | -2 | C. | 0或-2 | D. | -1或1 |
6.(-2)2的平方根是( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 4 |
 已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.
已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.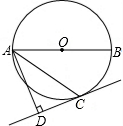 如图,AB是⊙O的直径,C为⊙O上一点,AD和过点C的切线CD垂直,垂足为点D.求证:AC平分∠BAD.
如图,AB是⊙O的直径,C为⊙O上一点,AD和过点C的切线CD垂直,垂足为点D.求证:AC平分∠BAD.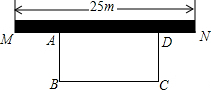 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在欲砌50m长的墙,砌成一个面积300m2的矩形花园,则BC的长为20 m.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在欲砌50m长的墙,砌成一个面积300m2的矩形花园,则BC的长为20 m.