题目内容
4．
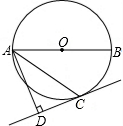如图，AB是⊙O的直径，C为⊙O上一点，AD和过点C的切线CD垂直，垂足为点D．求证：AC平分∠BAD．
分析 连接OC，如图，根据切线的性质得OC⊥CD，而AD⊥CD，根据平行线的判定方法得到OC∥AD，则∠2=∠3，加上∠1=∠3，所以∠1=∠2．
解答 
证明：连接OC，如图，
∵CD 是⊙O的切线，
∴OC⊥CD，
∵AD⊥CD，
∴OC∥AD，
∴∠2=∠3，
∵OA=OC，
∴∠1=∠3，
∴∠1=∠2，
∴AC平分∠BAD．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
相关题目
13．下面是一家商店四年盈亏情况统计表：（单位：万元）
补全该表，并进一步诊断一下，该商店这四年盈利还是亏损？
| 年 | 上半年盈利 | 下半年盈利 | 算式 | 合计 |
| 第一年 | 1.2 | 0.8 | 1.2+0.8 | |
| 第二年 | -0.6 | -0.7 | （-0.6）+（-0.7） | |
| 第三年 | -0.5 | 0.5 | （-0.5）+0.5 | |
| 第四年 | 0.9 | -0.1 | 0.9+（-0.1） |
19．
把一副直角三角板ABC（含30°、60°角）和CDE（含45°、45°角）如图放置，使直角顶点C重合，若DE∥BC，则∠1的度数是（ ）
把一副直角三角板ABC（含30°、60°角）和CDE（含45°、45°角）如图放置，使直角顶点C重合，若DE∥BC，则∠1的度数是（ ）| A． | 75° | B． | 105° | C． | 110° | D． | 120° |
9．下列运算正确的是（ ）
| A． | $\sqrt{4}=±2$ | B． | （-3）3=27 | C． | $\sqrt{4}$=2 | D． | $\root{3}{9}$=3 |
如图，CD⊥AB于D，点F是BC上任意一点，FE⊥AB于E，且∠1=∠2，∠3=80°，∠A=40°．
（尺规作图，不用写作法，保留作图痕迹）
14．下列运算正确的是（ ）
| A． | a•a2=a2 | B． | a2+a2=a4 | C． | a6÷a2=a3 | D． | （2a）2=4a2 |