题目内容
2.解决下列问题:已知二次根式$\sqrt{2{x}^{2}+2}$
(1)当x=3时,求$\sqrt{2{x}^{2}+2}$的值.
(2)若x是正数,$\sqrt{2{x}^{2}+2}$是整数,求x的最小值.
(3)若$\sqrt{2{x}^{2}+2}$和$\sqrt{2{x}^{2}+x+4}$是两个最简二次根式,且被开方数相同,求x的值.
分析 (1)根据题意可以求得$\sqrt{2{x}^{2}+2}$的值;
(2)根据x是正数,$\sqrt{2{x}^{2}+2}$是整数,可以求得x的最小值;
(3)根据$\sqrt{2{x}^{2}+2}$和$\sqrt{2{x}^{2}+x+4}$是两个最简二次根式,且被开方数相同,可以求得x的值.
解答 解:(1)当x=3时,
$\sqrt{2{x}^{2}+2}$=$\sqrt{2×{3}^{2}+2}=\sqrt{20}=2\sqrt{5}$;
(2)∵x是正数,$\sqrt{2{x}^{2}+2}$是整数,
∴$\sqrt{2{x}^{2}+2}$的最小值是2,
解得,x=1或x=-1(舍去),
即x的最小值是1;
(3)∵$\sqrt{2{x}^{2}+2}$和$\sqrt{2{x}^{2}+x+4}$是两个最简二次根式,且被开方数相同,
∴2x2+2=2x2+x+4,
解得,x=-2,
即x的值是-2.
点评 本题考查同类二次根式,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.实数16的平方根是( )
| A. | 4 | B. | ±4 | C. | 2$\sqrt{2}$ | D. | ±2$\sqrt{2}$ |
10.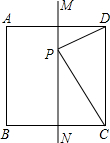 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
7.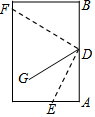 小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )
小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )
 小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )
小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 120° |
14.平面直角坐标系中,已知A(8,0),△AOP为等腰三角形且面积为16,满足条件的P点有( )
| A. | 12个 | B. | 10个 | C. | 8个 | D. | 6个 |