如图.MN是正方形ABCD的一条对称轴.点P是直线MN上的一个动点当PC+PD最小时.∠PCD=( )°．A．60°B．45°C．30°D．15° 题目和参考答案——青夏教育精英家教网—

题目内容

10．

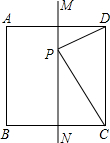如图，MN是正方形ABCD的一条对称轴，点P是直线MN上的一个动点当PC+PD最小时，∠PCD=（　　）°．

A．

60°

B．

45°

C．

30°

D．

15°

分析连接BD交MN于P′，如图，利用两点之间线段最短可得到此时P′C+P′D最短，即点P运动到P′位置时，PC+PD最小，然后根据正方形的性质求出∠P′CD的度数即可．

解答解：连接BD交MN于P′，如图，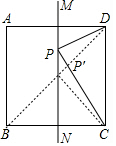
∵MN是正方形ABCD的一条对称轴，
∴P′B=P′C，
∴P′C+P′D=P′B+P′D=BD，
∴此时P′C+P′D最短，即点P运动到P′位置时，PC+PD最小，
∵点P′为正方形的对角线的交点，
∴∠P′CD=45°．
故选B．

点评本题考查了最短路线问题：在直线L上的同侧有两个点A、B，在直线L上有到A、B的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L的交点就是所要找的点．也考查了正方形的性质．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

1．下列给出的方程：①（x+1）（x-1）-x²=0；②x²+1=0；③y²-2y-1=0；④x²-1=$\frac{1}{x}$．其中是一元二次方程的是（　　）

a²+a³=2a⁵

a⁶÷a²=a³

a²•a³=a⁵

（2ab²）³=6a³b⁶

5．在Rt△ABC中，已知∠C=90°，AC=12，BC=5，则cosA等于（　　）

15．二次函数y=ax²-2ax+c的图象经过点（-1，0），则方程ax²-2ax+c=0解为（　　）

x₁=-3 x₂=-1

x₁=1 x₂=3

x₁=-1 x₂=3

x₁=-3 x₂=1

2．解决下列问题：
已知二次根式$\sqrt{2{x}^{2}+2}$
（1）当x=3时，求$\sqrt{2{x}^{2}+2}$的值．
（2）若x是正数，$\sqrt{2{x}^{2}+2}$是整数，求x的最小值．
（3）若$\sqrt{2{x}^{2}+2}$和$\sqrt{2{x}^{2}+x+4}$是两个最简二次根式，且被开方数相同，求x的值．

19．

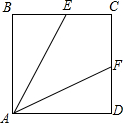如图，点E、F位于正方形ABCD边BC、CD上．
（1）当BE：EC=2：1，∠EAF=30°时，求CF：FD的值；
（2）若tan∠BAE=$\frac{1}{2}$，tan∠DAF=$\frac{1}{3}$，求∠EAF的度数．

20．下列代数式：-$\frac{1}{3}$，$\frac{3}{a}$，-π，-5x²y²$•\frac{2x{y}^{2}}{3}$$•\frac{a+b}{2}$，$\frac{1}{2}-x$，$\frac{5}{x+3}$，其中属于单项式的有-$\frac{1}{3}$，-π；属于多项式的有-5x²y²$•\frac{2x{y}^{2}}{3}$$•\frac{a+b}{2}$，$\frac{1}{2}-x$；属于整式的有-$\frac{1}{3}$，-π，-5x²y²$•\frac{2x{y}^{2}}{3}$$•\frac{a+b}{2}$，$\frac{1}{2}-x$．

试题分类