题目内容
3.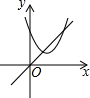 已知正比例函数y=x与二次函数y=ax2+bx+c的图象如图所示,则二次函数y=ax2+(b-1)x+c的图象可能是( )
已知正比例函数y=x与二次函数y=ax2+bx+c的图象如图所示,则二次函数y=ax2+(b-1)x+c的图象可能是( )| A. |  | B. | 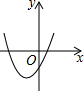 | C. | 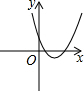 | D. | 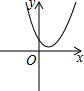 |
分析 由图象可知一次函数y=x与二次函数y=ax2+bx+c交于第一象限的P、Q两点,方程ax2+(b-1)x+c=0有两个正实数根,得到结论.
解答 解:如图,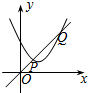
∵点P在抛物线上,设点P(x,ax2+bx+c),又因点P在直线y=x上,
∴x=ax2+bx+c,
∴ax2+(b-1)x+c=0;
由图象可知一次函数y=x与二次函数y=ax2+bx+c交于第一象限的P、Q两点,
∴方程ax2+(b-1)x+c=0有两个正实数根,
∴函数y=ax2+(b-1)x+c的图象与x轴有两个交点,并且这两个交点都在x轴的正半轴上,
符合条件的只有选项C,
故选C.
点评 此题是二次函数图象题,主要考查了正比例函数与二次函数y=ax2+bx+c的图象,以及交点坐标的位置,正确识图是解本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
14.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.已知am=9,am-n=3,则an的值是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | 1 |
18.下列计算正确的是( )
| A. | 3a-a=3 | B. | a2+a2=a4 | C. | (3a)-(2a)=6a | D. | (a2)3=a6 |
8.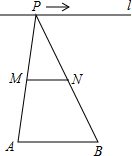 如图,点A,B为定点,定直线l∥AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④∠APB的大小.其中随点P的移动不会变化的是( )
如图,点A,B为定点,定直线l∥AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④∠APB的大小.其中随点P的移动不会变化的是( )
 如图,点A,B为定点,定直线l∥AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④∠APB的大小.其中随点P的移动不会变化的是( )
如图,点A,B为定点,定直线l∥AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④∠APB的大小.其中随点P的移动不会变化的是( )| A. | ①② | B. | ②④ | C. | ①③ | D. | ①④ |
15.已知a、b满足a+b=5且ab=6,以a、b为根的一元二次方程为( )
| A. | x2+5x+6=0 | B. | x2-5x+6=0 | C. | x2-5x-6=0 | D. | x2+5x-6=0 |
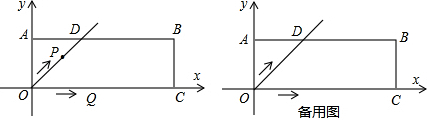
 如图,AB∥ED,∠B+∠C+∠D=360°.
如图,AB∥ED,∠B+∠C+∠D=360°. 如图,平行四边形ABCD,请你添一个条件∠A=90°,使四边形ABCD为矩形.
如图,平行四边形ABCD,请你添一个条件∠A=90°,使四边形ABCD为矩形.