题目内容
11.(1)计算:$|{-2}|-{({-2})^{-2}}-{({\sqrt{2012}-2013})^0}$.(2)解方程:$\frac{x^2}{{{{({x-2})}^2}}}-\frac{2x}{x-2}-3=0$.
分析 (1)根据绝对值,负指数幂,0次幂计算即可解答;
(2)令$\frac{x}{x-2}$=a,方程转化为a2-2a-3=0,解出a的值,再求关于x的方程.
解答 解:(1)|-2|-(-2)-2-$(\sqrt{2012}-2013)^{0}$
=2-$\frac{1}{4}$-1
=-$\frac{3}{4}$.
(2)令$\frac{x}{x-2}$=a,方程转化为a2-2a-3=0,
解得:a1=3,a2=-1,
当a=3时,$\frac{x}{x-2}$=3,
解得:x=3,
检验:当x=3时,x-2≠0,所以x=3是方程的解;
当a=-1时,$\frac{x}{x-2}$=-1,
解得:x=1,
检验:当x=1时,x-2≠0,所以x=1是方程的解;
所以方程的解为:x1=3,x2=1.
点评 本题考查了实数的运算和解方程,在解决(2)中的关键是令$\frac{x}{x-2}$=a,方程转化为a2-2a-3=0,解出a的值,再求关于x的方程.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
19.小馨和小霏是七(1)班的学生,两人既是好朋友,又是学习上的竞争对手.她们约定在本次的期末考试中比一比谁的总分高.(考试科目见下表,每门课的满分为100分,单科分数均为整数)下表是她们期末考试的部分成绩.
根据表格显示的数据,小霏同学数学成绩至少91 分,她的总分才有可能比小馨总分高.
| 姓名 | 语文 | 数学 | 英语 | 政治 | 历史 |
| 小馨 | 86 | 98 | 100 | 96 | 97 |
| 小霏 | 88 | 99 |
6.若点P在第四象限,且P到x轴的距离为1,到y轴的距离为2,则点P的坐标是( )
| A. | (-1,2) | B. | (1,-2) | C. | (-2,1) | D. | (2,-1) |
3.下列计算正确的是( )
| A. | a3+a2=a5 | B. | a3-a2=a | C. | a2•a4=a8 | D. | a3÷a2=a |
1.已知a,b都是整数,且满足a2+b2+1<2a-2b,则a+b=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,如果AB∥CD,∠B=30°,∠D=30°,那么BC与DE平行吗?为什么?
如图,如果AB∥CD,∠B=30°,∠D=30°,那么BC与DE平行吗?为什么?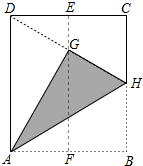 如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为2$\sqrt{3}$cm.
如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为2$\sqrt{3}$cm.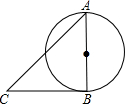 如图,AB是⊙O直径,BC是⊙O的切线,AB=BC,求∠A的度数.
如图,AB是⊙O直径,BC是⊙O的切线,AB=BC,求∠A的度数.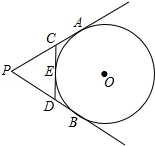 如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.
如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.