题目内容
16.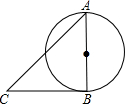 如图,AB是⊙O直径,BC是⊙O的切线,AB=BC,求∠A的度数.
如图,AB是⊙O直径,BC是⊙O的切线,AB=BC,求∠A的度数.
分析 先根据切线的性质得∠ABC=90°,再判断△ABC为等腰直角三角形,然后根据等腰直角三角形的性质求解.
解答 解:∵BC是⊙O的切线,
∴AB⊥BC,
∴∠ABC=90°,
∵AB=CB,
∴△ABC为等腰直角三角形,
∴∠A=45°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了等腰直角三角形的判定与性质.

练习册系列答案
相关题目
7.在△ABC和△A′B′C′中,①AB=A′B′,②BC=B′C′,③AC=A′C′,④∠A=∠A′,⑤∠B=∠B′,⑥∠C=∠C′,则下列条件中不能保证△ABC≌△A′B′C′的是( )
| A. | ①②③ | B. | ①②⑤ | C. | ①⑤⑥ | D. | ①②④ |
6.下列计算正确的是( )
| A. | 3ab-2ab=1 | B. | ($\sqrt{2}$+1)(1-$\sqrt{2}$)=1 | C. | -(-a)4÷a2=a2 | D. | $\root{3}{-8}$=-2 |
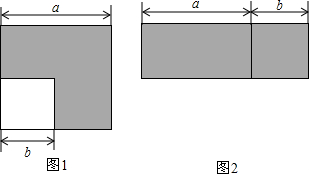 如图1,在边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形.
如图1,在边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形. 在A、B、C、D四幅图案中,哪一幅可以通过平移(1)得到( )
在A、B、C、D四幅图案中,哪一幅可以通过平移(1)得到( )



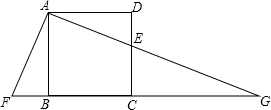 如图,E是正方形ABCD的边DC上的一点,过点A作AF⊥AE,交CB延长线于点F,AE的延长线交BC的延长线于点G.若AF=7,DE=2,则EG的长是$\frac{21\sqrt{5}}{2}$-7.
如图,E是正方形ABCD的边DC上的一点,过点A作AF⊥AE,交CB延长线于点F,AE的延长线交BC的延长线于点G.若AF=7,DE=2,则EG的长是$\frac{21\sqrt{5}}{2}$-7.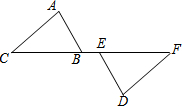 如图,点C、B、E、F在同一直线上,CE=BF,AC∥DF,AC=DF.求证:△ABC≌△DEF.
如图,点C、B、E、F在同一直线上,CE=BF,AC∥DF,AC=DF.求证:△ABC≌△DEF.